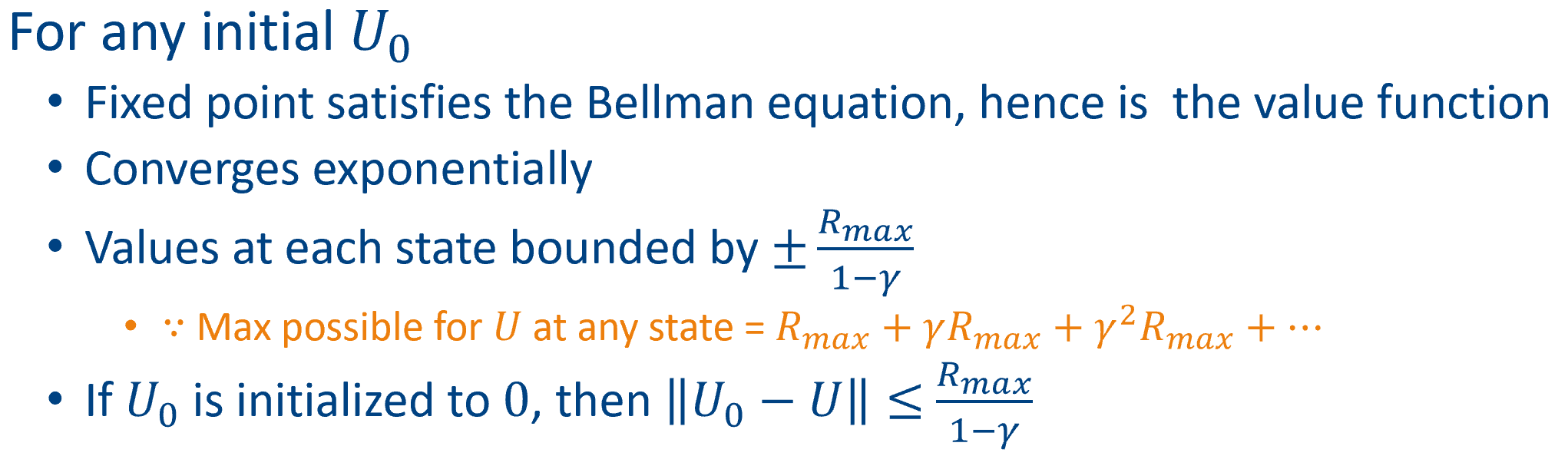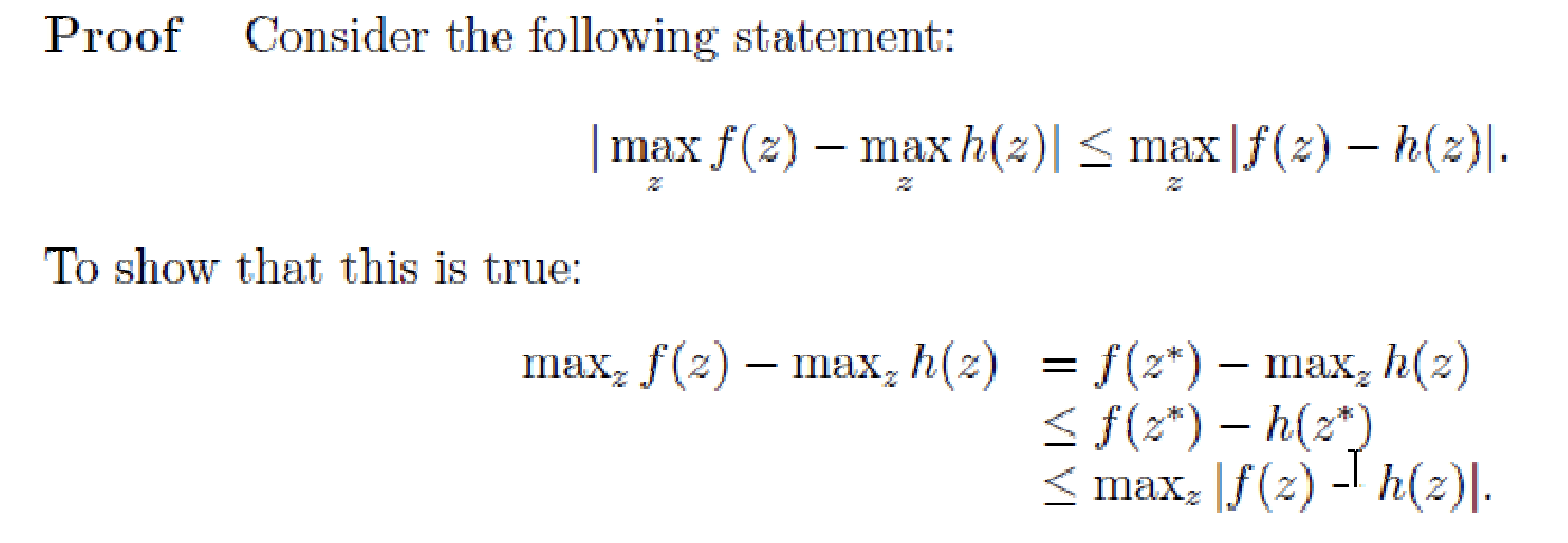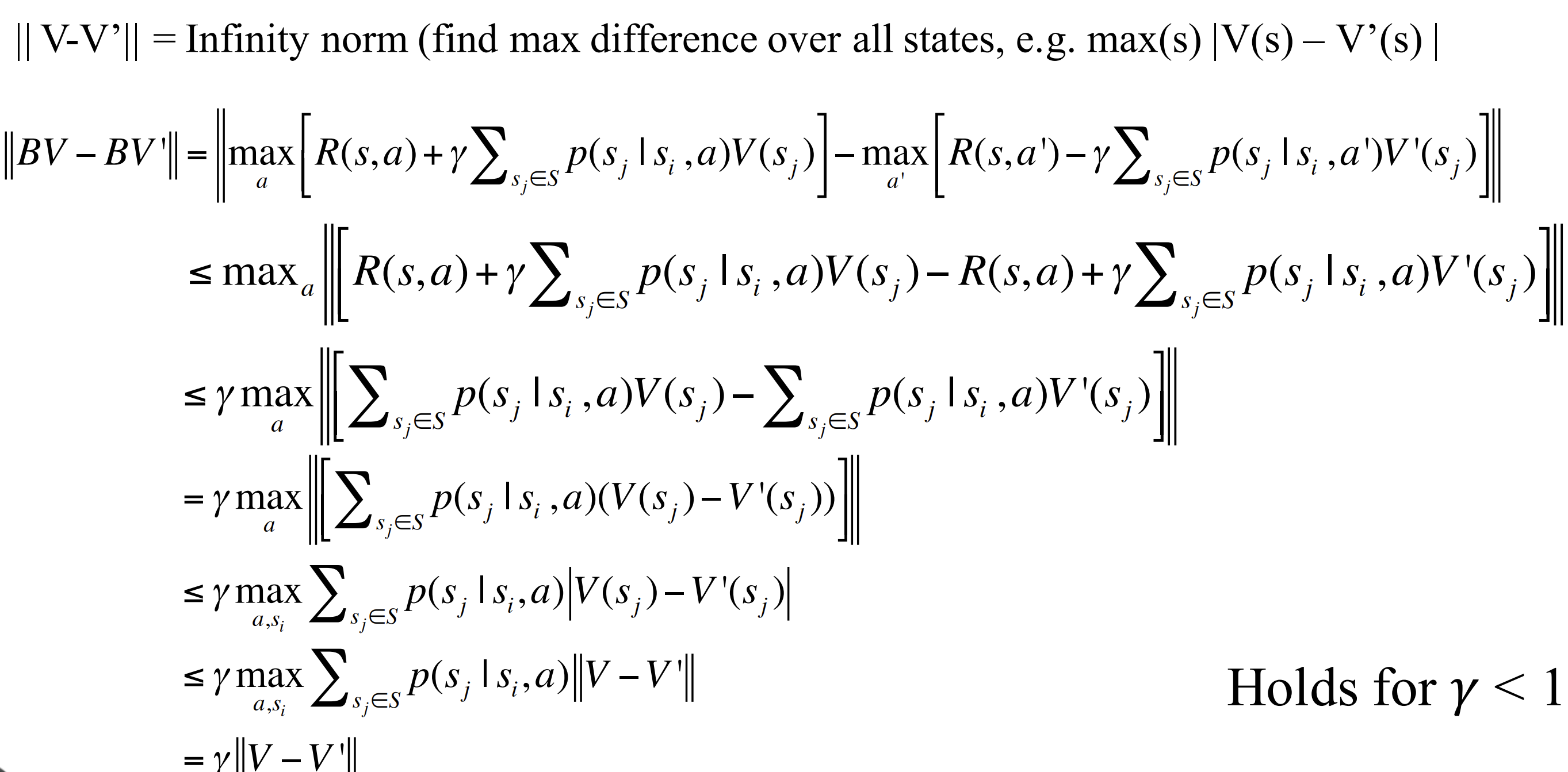Sequential decision problems
Deals with fully observable and partially observable cases.
Markovian assumption: Probability depends only on current state $s$ not the history of earlier states.
Markov decision process (MDP): A sequential decision problem for a fully observable stochastic environment with Markovian transition and additive rewards.
MDP: $(S, A, T, R)$
A set of states, $S$, with initial state $s_0$
A set of actions, $A$
A transition model, $T$, defined by $P(s’|s,a)$, outcomes of actions are stochastic.
A reward function, $R(s)$ (sometimes, more generally: $R(s,a,a’)$, Utility function depends on sequence of states while each state has a corresponding reward 𝑅(𝑠)
Policy($\pi (s)$) is a solution to MDP(a function from state to action) and is not unique. It is a mapping given whatever state in a system and output appropriate actions.
The difference is how good these policies are(quality of the policy): measured by the expected return(Expected utility of possible state sequence generated by the policy).
Optimal policy $\pi^{*}$: policy that generates highest expected utility.
Ways to evaluate
Finite horizon:
- fixed time $N$ and terminate,
- return is usually the addition of rewards over the sequence:
- optimal action at a state can change depending on how many steps remain,
- optimal policy is non-stationary.
Infinite horizon:
- no fixed time limit,
- optimal action depends only current state: stationary.
- comparing utilities are difficult: utilities can be infinite.
- discounted rewards: (bounded by $\pm R_{max}$)
- Expected utility of executing $\pi$ starting from $s$:Optimal policy:Number of policies $\pi$ is finite if the number of states is finite.
$n$ states and $a$ actions lead to $a^n$ policies.
Value function
Value of optimal policy is called value function $U^{\pi^{*}}(s)$
Given the value function, we can compute an optimal policy as:
Value iteration
What if the agent performs suboptimally on purpose? Is the agent still rational? (eg. taking longer route to reduce the probability of utility loss)
State variables: factorced representation, each variable can have various values;
State: atomic representation, each variable is set to be a specific value. A state is an assignment of state variable.
Fixed point algorithm: run the algorithms many times and it will finally converge to a fixed result ($\gamma < 1$). The algorithm comes to an end when the utility function no longer update.
If apply an operator to a function, it will be updated to another function.

Function – mapping from input to output. For finite domains, function is a vector
Operator – takes a function as input and gives another function as output
Contraction – distance between 2 functions reduce on applying an operator
Max norm : $||U||=\max_s U(s)$
Bellman operator $B$: $R^{|s|}\Rightarrow R^{|s|}$
$T$ is the transition matrix and $V$ is the value matrix.
Lemma 1: Bellman operation is a contraction
Lemma 2: Value Iteration converges to $V^{\pi}$ with any initial estimate $V$
Property of convergence: $\forall t, H^t(V^{\pi}) = V^{\pi}$
After $N$ iterations:
which is equivalent to:
When $N$ is large enough, the right side of the inequality approaches zero, and the value matrix converge to $V^{\pi}$.
$H^t(V)$: apply bellman operator to $V$ for $t$ times
Time needed to converge:
The max initial error is:
After $N$ iteration:
Termination condition is for error to be small enough:
Approximate Policy Evaluation
proof:
So the terminate condition with a discount factor $\gamma$ is :
All MDP can be solved by value iteration in theory, but in practice if there are too many states it cannot be solved.
Policy iteration
Problem with VI: Exact algorithm + Scales poorly
VI compute the utility of each state exactly, but to get an optimal solution we only need to know if one action is clearly better than others. So PI is doing ordering of policies.
Policy evaluation – given a policy $\pi_i$, calculate $U_i = U^{\pi_i}$, if $\pi_i$ is executed.
Policy improvement – calculate new policy $\pi_{i + 1}$ using one-step look ahead based on $U_i$.
Terminate when there is no change in the policy (must terminate since the number of policies is finite).
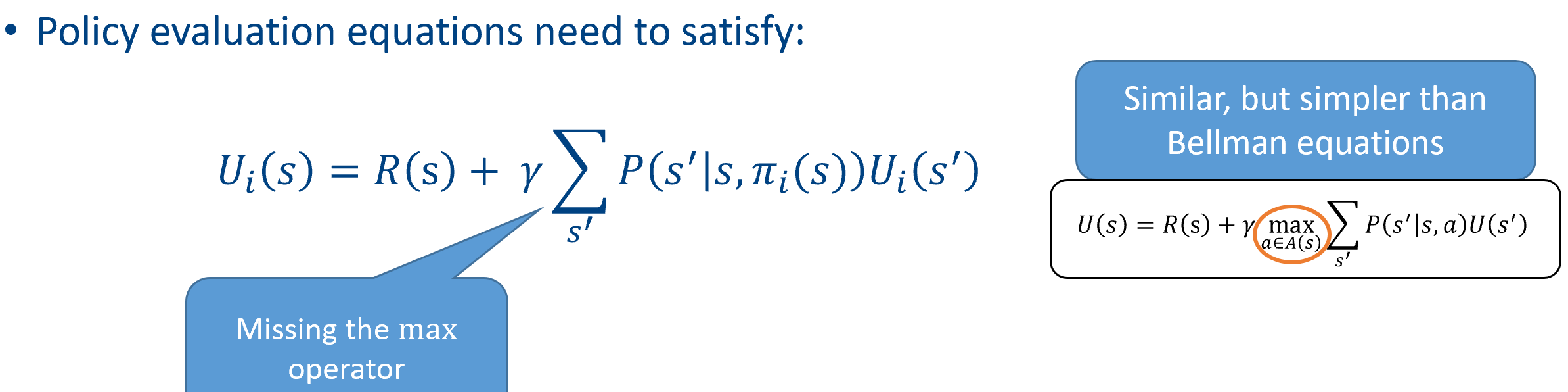

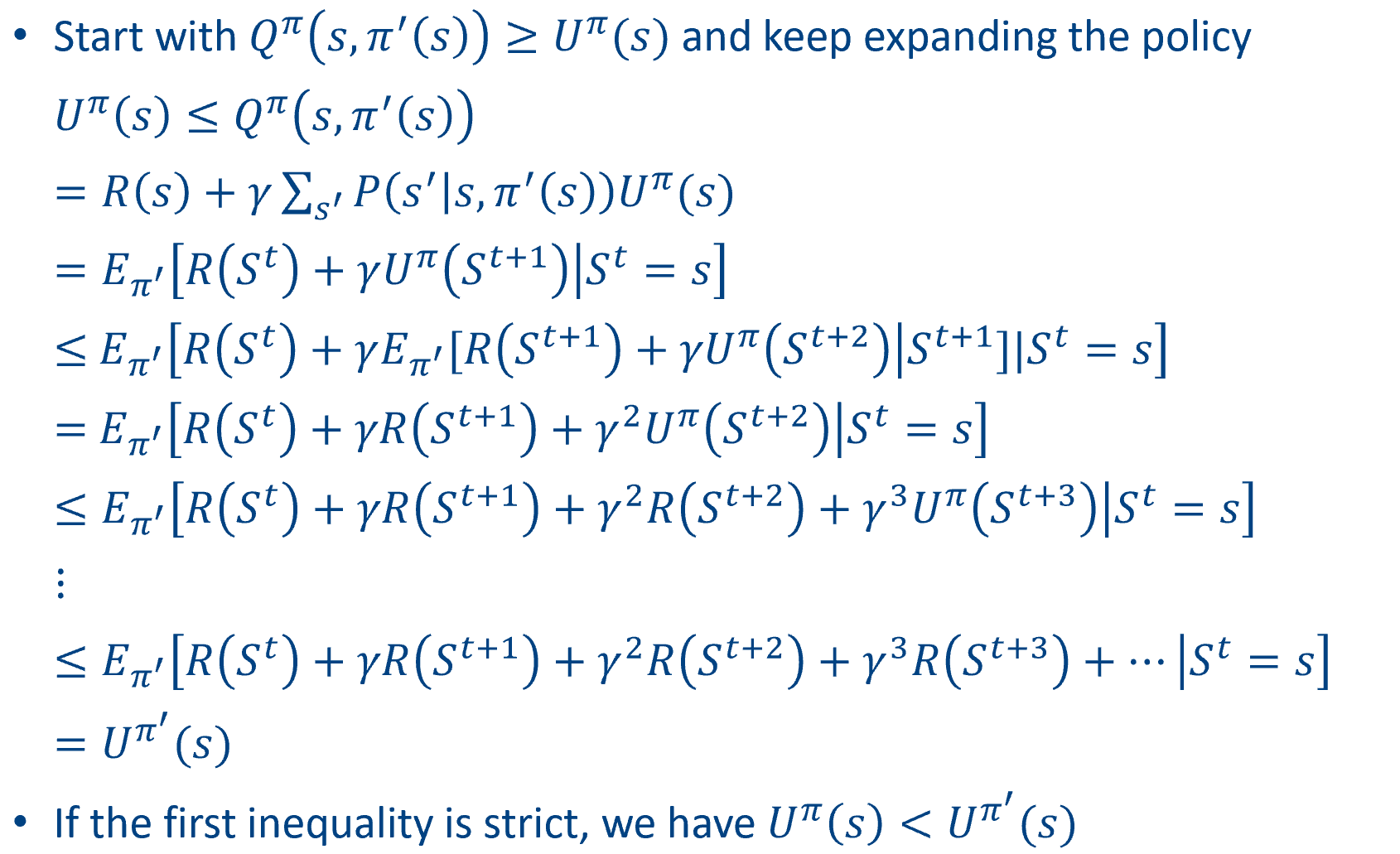
Improving policy iteration
Modified policy iteration
Do only $k$ iterations instead of going to convergence.
Evaluate approximately.
Asynchronous policy iteration
Pick only a subset of states for either policy improvement or for updating in policy evaluation.
Converges as long as we continuously update all states.
Generalized policy iteration (a general scheme of solution)
Update value according to policy, and improve policy WRT the value function.
VI, PI, Async-PI are all special cases of GPI.
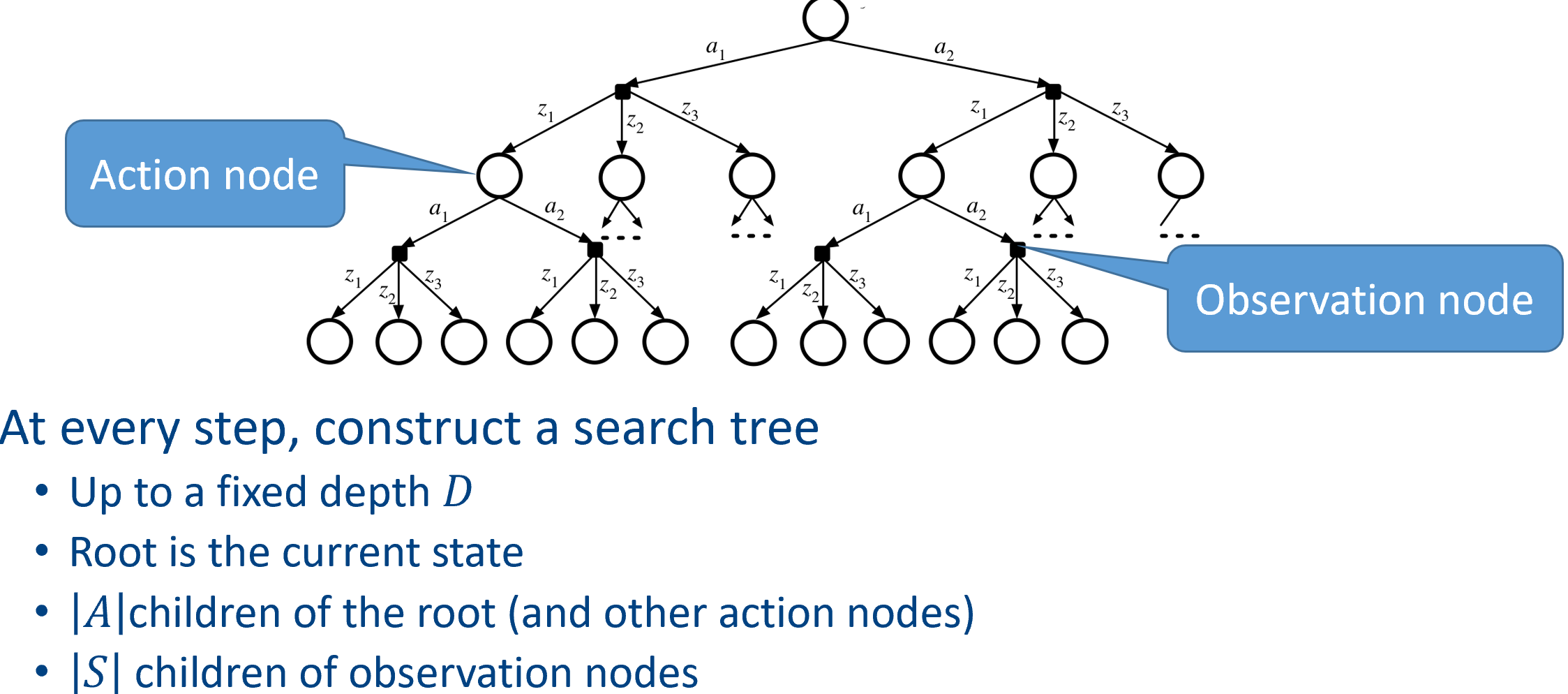
Online search
VI/PI iterates through all states, exponential with the number of variables
To handle curse of dimensionality
- Use function approximation
Linear function of features
Deep neural networks - Do online search with sampling

Some other resources
https://people.eecs.berkeley.edu/~pabbeel/cs287-fa09/lecture-notes/lecture5-2pp.pdf
https://www.cs.cmu.edu/~arielpro/15381f16/c_slides/781f16-11.pdf
Within one iteration: