Planning Graphs
Search trees grow exponentially large very fast. Depth at which the goal first appears means the minimum number of steps required to achieve the goal.
Planning graph is a polynomial sized approximation to the search tree.
$S_i$ contains all literals that could hold at time $i$ and $A_i$ contains all actions that could have their preconditions satisfied at time $i$.
The level at which a literal first appears is a good estimate of how difficult it is to achieve the literal. The graph can also estimates which set of propositions are reachable from $S_0$ with which actions.
Planning graphs work only on propositional planning problems – need to propositionalize PDDL action schemas.
Propositionalize the actions: replace each action schema with a set of ground actions formed by substituting constants for each of the variables. These ground actions are not part of the translation, but will be used in subsequent steps.
Construct a planning graph
Level off – the graph is constructed until two consecutive levels are identical - constructed level by level
Search tree:
- one action at each level; branch on each action
- gives true depth when goal is achieved
Planning graph:
- all actions that have preconditions satisfied appear in parallel and produce all possible effects
No need to choose among actions
Records if some choices are impossible - optimistic estimate of goal depth
Goal: Construct a plan where at each time step, have such a set of actions
Planning graph – search for plan with parallel actions OR usual plan search
Properties
For a planning graph with $l$ literals and $a$ actions,
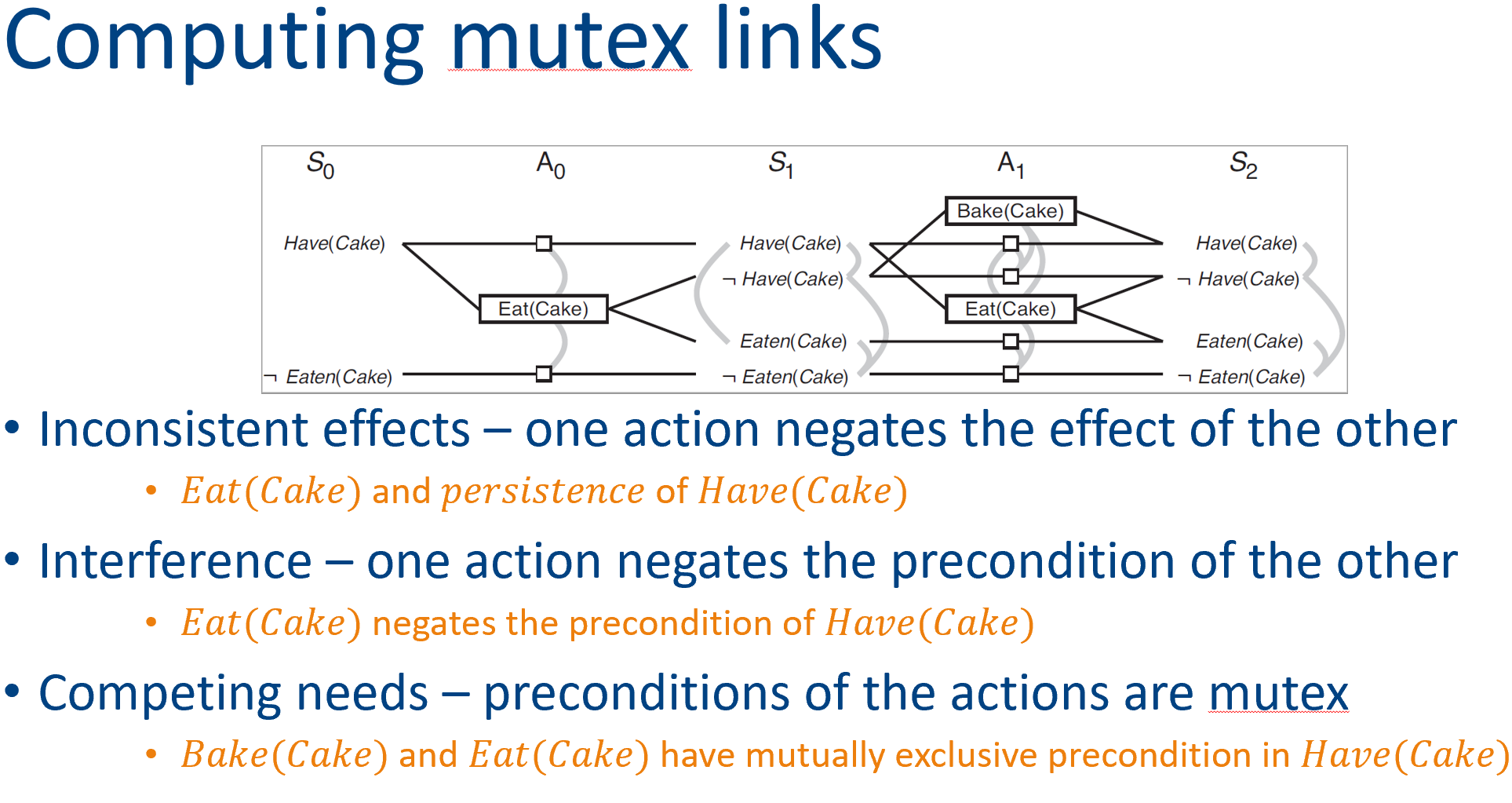
Each $S_i$ has at most $l$ nodes and $O(l^2)$ mutex links
Each $A_i$ has at most $a+l$ nodes (including no-op), $(a+l)^2$ mutex links, and $2(al+l)$ precondition and effect links
Entire graph with $n$ levels has size $𝑂(n(a+l)^2)$
Same complexity for time to build the graph

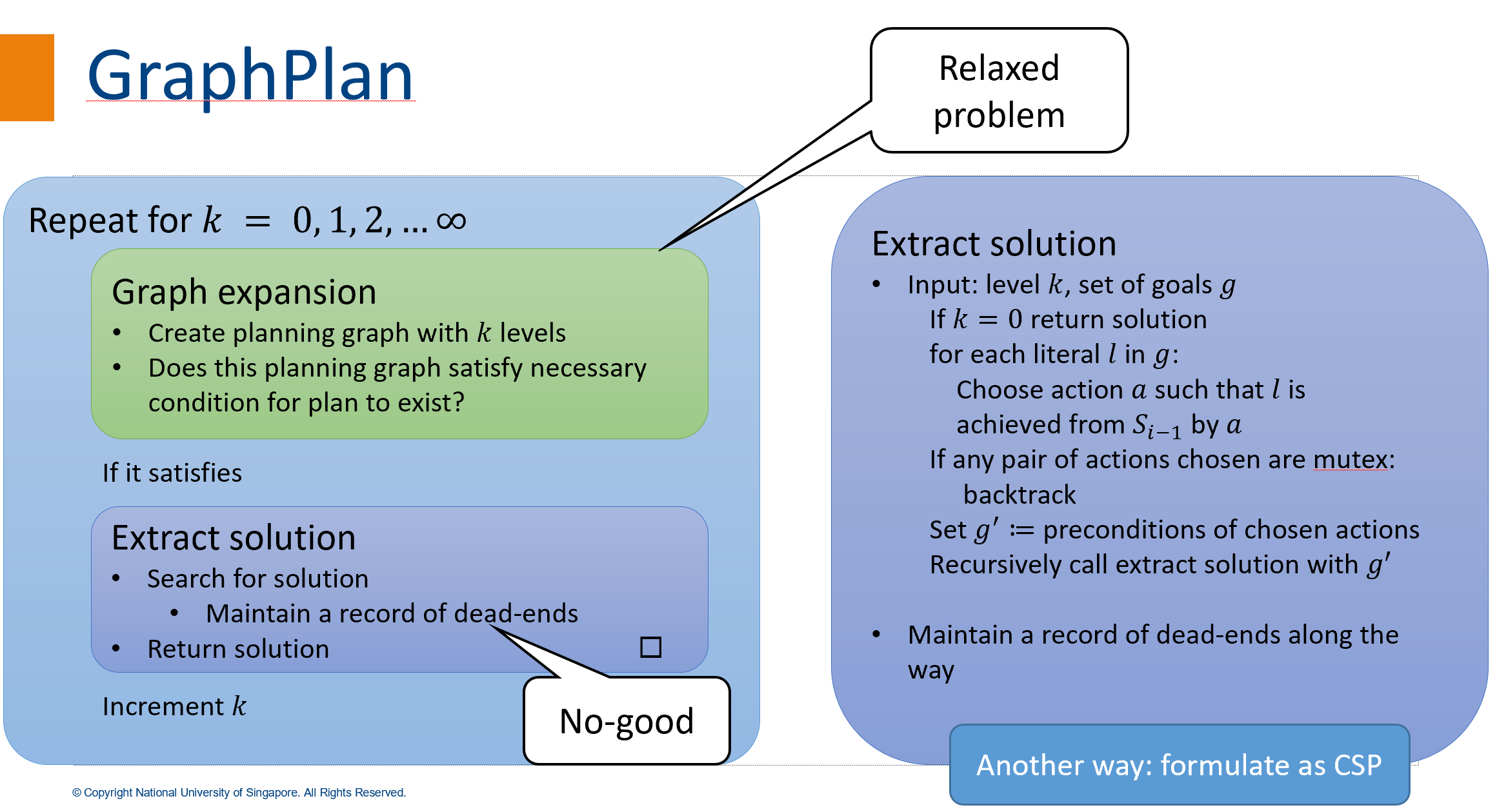
GraphPlan algorithm
A planning graph is a polynominal approximation of the search tree, which means it is much smaller than a search tree for the same planning problem.
Constructed level by level.
Constrained by mutex links.
Two-stage: limit the search space + search for solution
Expand the graph, if the goal is satisfied, extract the solution(similar to backward search)