Decision Theory 1

Uncertainty

The real environment is full of uncertainty.
Partial observability(traffic) + non-determinism(car break down)

Utility theory

“How agent can make a rational decision in a random environment?”
Question for machine is what a rational decision is and how to make rational decisions.

Axiomatic approach
We say something about the environment and assert they are always true.
To define the axioms: start with preferences between outcomes $A$ and $B$. Based on the preferences, agents can make a choice.
$A>B$: agent prefers $A$ over $B$ (Partial order)
$A\sim B$: agent is indifferent between $A$ and $B$
$A\ge B$: agent prefers $A$ over $B$ or is indifferent

Utility – consequence of the preference
A function $U$, for any $A,B\in S$ (outcomes in one domain):

$$U(A)>U(B)\Leftrightarrow A>B$$ $$U(A)=U(B)\Leftrightarrow A\sim B$$

Function $U$ is not unique, any monotonically increasing transformation will preserve the preference relation.

Lottery is to model the state of chance.
A lottery $L$ with outcomes $S_1,S_2,…,S_n$ that occur with probabilities $p_1,p_2,…,p_n$ is denoted as:

$$L=[p_1,S_1;p_2,S_2;...p_n,S_n]$$

Each of the outcome $S_i$ can be an atomic state or another lottery(another probability).

Axioms of Utility theory

Axiom 1: Orderability or Completeness

Given any 2 outcomes $A,B\in S$, exactly one of the following holds:
$𝐴>B$, $B>A$ and $A\sim B$.

Axiom 2: Transitivity

If the agent prefers $A$ to $B$ and $B$ to $C$, then the agent must prefer $A$ to $C$(Similarly for $\sim$):

$$(A>B)\wedge (B>C)\Rightarrow A>C$$ $$(A\sim B)\wedge (B\sim C)\Rightarrow A\sim C$$

If the order is circle, the transitivity is broken, and the agent is behaving irrationally.
Group preference may be non-transitive, studied in social choice theory

Axiom 3: Continuity

If $B$ is in between $A$ and $C$ in preference, there must be a probability $p$, such that the agent is indifferent to:

$$A>B>C\Rightarrow\exists p [p,A;(1-p),C]\sim B$$

Axiom 4: Substitutability

If an agent is indifferent between two lotteries $A$ and $B$, the agent is indifferent to two complex lotteries that are the same, except $B$ is substituted for $A$ in one of the (Similarly for preference):

$$A\sim B\Rightarrow [p,A;(1-p),C]\sim [p,B;(1-p),C]$$

Axiom 5: Monotonicity

Prefer higher probability of getting prefered outcome:

$$A>B\Rightarrow ((p>q)\Leftrightarrow [p,A;(1-p),B]>[q,A;(1-q),B])$$

Axiom 6: Decomposability

Compound lotteries can be reduced to simpler ones using laws of probability:

$$[p,A;(1-p),[q,B;(1-q),C]]\sim [p,A;(1-p)q,B;(1-p)(1-q)C]$$

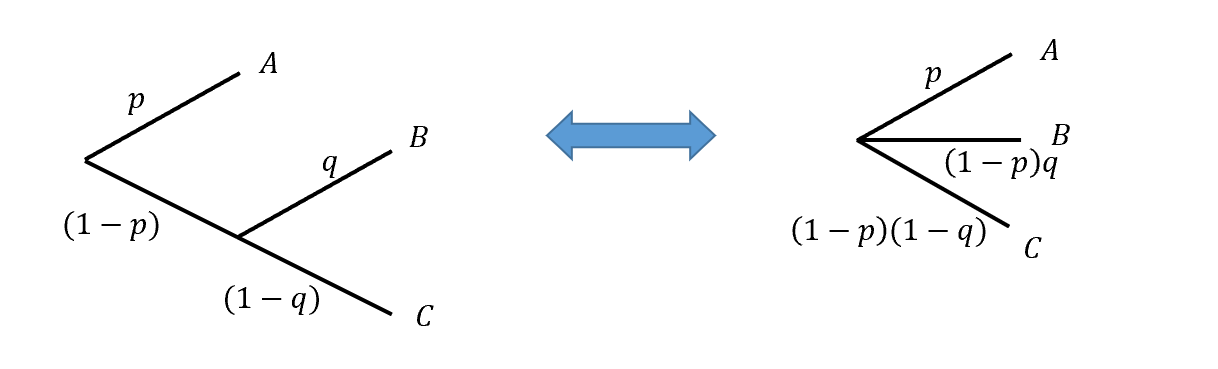
Axioms to consequence

1. Existence of Utility function
   If agent’s preferences obey the axioms of utility, then there exists a function 𝑈 such that, for any two lotteries 𝐴 and 𝐵:

   $$U(A)>U(B)\Leftrightarrow A>B$$ $$U(A)\sim U(B)\Leftrightarrow A\sim B$$

2. Expected Utility of a lottery
   The utility of a lottery is the expected value of the utilities of the outcomes:

   $$U([p_1,S_1;...;p_n,S_n])=\sum_ip_iU(S_i)$$

3. Acting Rationally
   The agent acts rationally, i.f.f. it chooses the action that maximizes the expected utility.
   Agent’s behavior doesn’t change if $U$ is subjected to an affine transformation: $U’(s)=aU(s)+b$ with $a>0$.

An affine transformation is any transformation that preserves collinearity (i.e., all points lying on a line initially still lie on a line after transformation) and ratios of distances (e.g., the midpoint of a line segment remains the midpoint after transformation).

Rational agent

Maximum Expected Utility: Rational agent should choose the action that maximized its expected utility:

$$\arg\max_a EU(a|e)=\arg\max_a \sum_{s'}P(Result(a)=s'|a,e)U(s')$$

Human Irrationality:
Decision theory is normative – describe how ration agent should act.
Descriptive theory – describe how humans actually act.