Summary

Graph Models

DGM

UGM (MRF: Markov Random Field)

Markov Property:

• Global: no path between
• Local: condition upon Markov blanket
• Pair: given the rest, no direct edges

Intersection Lemma:

$$X\perp Y|\{W,Z\}\quad + \quad X\perp W|\{Y,Z\}\quad\to\quad X\perp\{Y,W\}|Z$$

$X\perp Y|\{W,Z\}$: $p(X,Y,Z,W)=f_{XWZ}(X,W,Z)f_{WYZ}(W,Y,Z)$
$X\perp W|\{Y,Z\}$: $p(X,Y,Z,W)=g_{XYZ}(X,Y,Z)g_{WYZ}(W,Y,Z)$
$X\perp\{Y,W\}|Z$: $p(X,Y,Z,W)=\mu_{XZ}(X,Z)\mu_{WYZ}(W,Y,Z)$
Functions are valid factorizations, or a graph is a valid representation of distribution, if all independencies encoded in this graph is a subset of the distribution.

MRF does not preserve the local probabilitic interpretations(conditional probabilities like parent-child relation in DGM), but still has all important representation of the joint distribution.

$X_i$, $X_j$ that are not directly linked are independent given all the rest nodes, which means they should appear in different factors of the factorization of joint distribution.
In contrast, all nodes in the same maximal clique should appear together in one local function $\psi(x_c)$.

Joint probability can be factorized as the product of potential functions for all cliques $C$:

$$p(y|\theta)=\frac{1}{Z(\theta)}\prod_{c\in C}\psi_c(y_c|\theta_c)$$

Log-linear potetial is defined as:

$$log\psi_c(y_c|\theta)=\phi(y_c)^T\theta_c$$

The cliques can be choosen as maximal cliques, pairwise cliques(each edge forms a clique) and canonical cliques(all possible cliques).

• Generative Models: Likelihood — $p(x|C_k)$
• Discriminative Models: Likelihood — $p(C_k|x)$

CRF: Conditional Random Field (a special kind of UGM, discriminative model)

UGMs condition upon a global input $x$, $x_1,…,x_n$ are fully connected to each other:

$$p(y|x,w)=\frac{1}{Z(x,w)}\prod_{c\in C}\psi_c(y_c|x,w_c)$$ $$log\psi_c(y_c|x,w)=\phi(y_c,x)^Tw_c$$

So we have:

$$\begin{aligned} p(y|x,w)&=\frac{1}{Z(x,w)}\psi(y|x,w) \\&=\frac{exp(\phi(y,x_1,...,x_n)^Tw)}{\sum_y exp(\phi(y,x_1,...,x_n)^Tw)} \\&=\frac{exp(\sum_n \phi(y,x_n)w_n)}{\sum_y exp(\sum_n \phi(y,x_n)w_n)} \end{aligned}$$

where:

$$\phi(y=1,x_n)w_n=I(y^+)x_nw_n^+$$ $$\phi(y=0,x_n)w_n=I(y^-)x_nw_n^-$$

$I()$ is an indicate function that is used to choose from $w_n^+$ and $w_n^-$ according to the value of input($y^+$ or $y^-$).

$$\begin{aligned} p(y^+|x)&=\frac{exp(w_+^Tx)}{exp(w_+^Tx)+exp(w_-^Tx)}\qquad w'=w_+-w_- \\&=\frac{1}{1+exp(-w^{'T}x)}\qquad Logistic Regression! \end{aligned}$$

The equations above indicate that CRF can be transformed into a DNN when $w_+^Tx$ is a non-linear function $f(x;w)$:

$$p(y+|x)=\sigma(f(x;w))$$

The sigmoid function can be replaced by the softmax function for multi-class classification.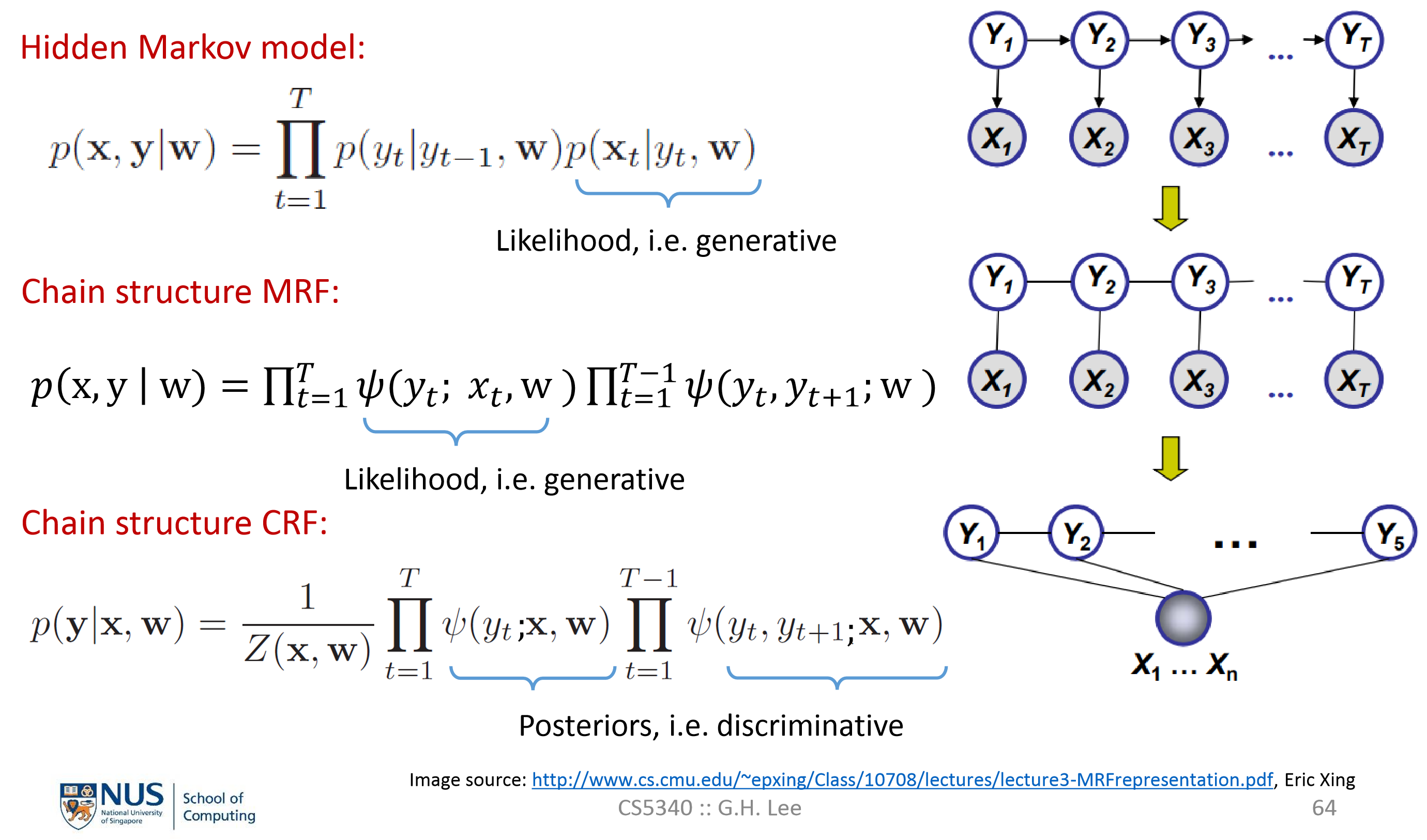

• Benefits of CRF:
  Make use of observations(data labels)
  Make the model ata-dependent(make the latent labels depend on global properties )
• Shortbacks of CRF:
  Require labeled training data
  Learning is slower

Inference for marginalization/conditional probability or maximum probability

Variable Elimination (query sensitive)

Junction Tree Algorithm

Factor Tree (solve the loopy problem)

Cluster Graph (convert to Junction Tree)

Parameter Learning