Variable Elimination Algorithm

General probabilistic problem: calculate $p(X_F|X_E)$ for arbitrary disjoint subsets $E$ and $F$: ( $X_F$ are query nodes, $X_E$ are evidence nodes)

$p(X_F|X_E)=\frac{p(X_F,X_E)}{p(X_E)}=\frac{\sum_{X_R}p(X_E,X_F,X_R)}{\sum_{X_F}p(X_F,X_E)}$

$X_R$ are nodes that must be marginalized out of joint probability.

Joint probability table size of $n$ variabels that takes $k$ states:
a naive summation: $O(k^n)$.
a factored form: $O(k^r)$ where $r\ll n$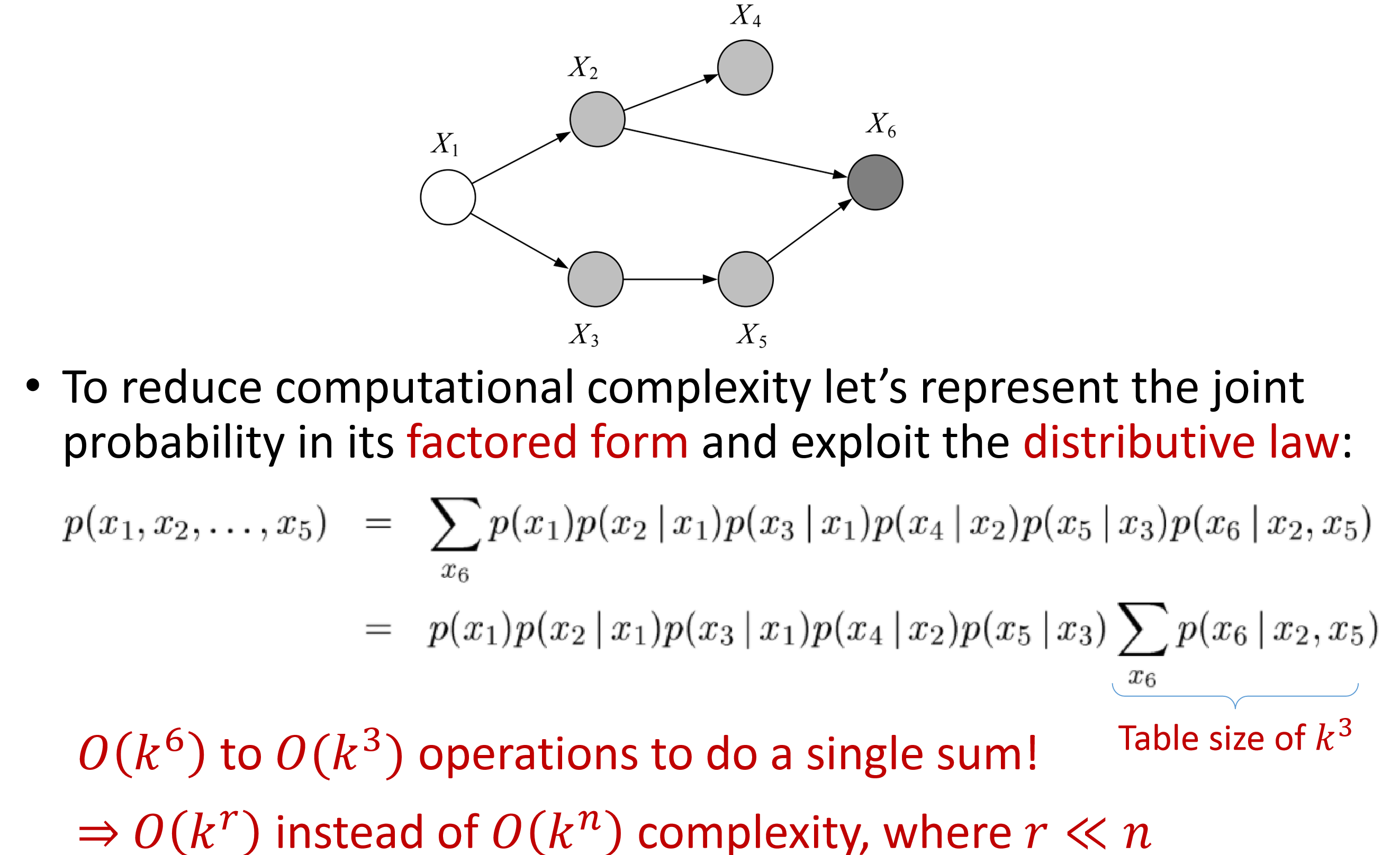

k^r

$p(X_6|X_2,X_5)$: 3d table
$p(\bar{X_6}=1|X_2,X_5)$: a 2d slice of the 3d table

Evidence potential:

$\delta(x_i,\bar{x_i})\begin{cases} 1,\qquad if\quad x_i = \bar{x_i} \\ 0,\qquad else\end{cases}$

Turn evaluation into sum:

$g(\bar{x_i})=\sum_{x_i}\delta(x,\bar{x_i})=g(x_i=\bar{x_i})$

Which means setting lines of table $p(x_i)$ where $x_i \neq \bar{x_i}$ to 0.
Evidence potential is a trick to simplify the description. In practice we take slices instead of doing summation.

Eliminate(G,E,F):

Initialize: choose elimination ordering, query nodes appear at the last.
Evidence: place evidence
Update: marginalization.
Loop: 1. $\phi_i = $ product of …, which is the unnormalized conditional probability. 2. $m_i(x_{S_i})=\sum_{x_i}\phi_i$, which is the narmalization factor.
Normalize(F) $p(x_F|\bar{x_E})=\frac{\phi_F(x_F)}{\sum_F\phi_F(x_F)}=\frac{\phi_F(x_F)}{m_F(x_{S_F})}$ For conditional probability, normalization factor Z cancels.
For a marginal probability, Z cannot be canceled.

elimination

Constituted Graph

Eliminate: removing the node from graph and connecting the remaining neighbors, thus creating “elimination cliques”.
Reconstitute: add additional edges during the elimination process to the original graph. (Complexity depends on the choice of elimination order)
Treewidth: one less than the smallest achievable cardinality of the largest elimination clique over all possible elimination ordering.

Computaional Complexity of DGM can be convert to UGM by moralization.

Limitation: re-run elimination algorithm for every new query nodes, since different query nodes require different eliminate order.

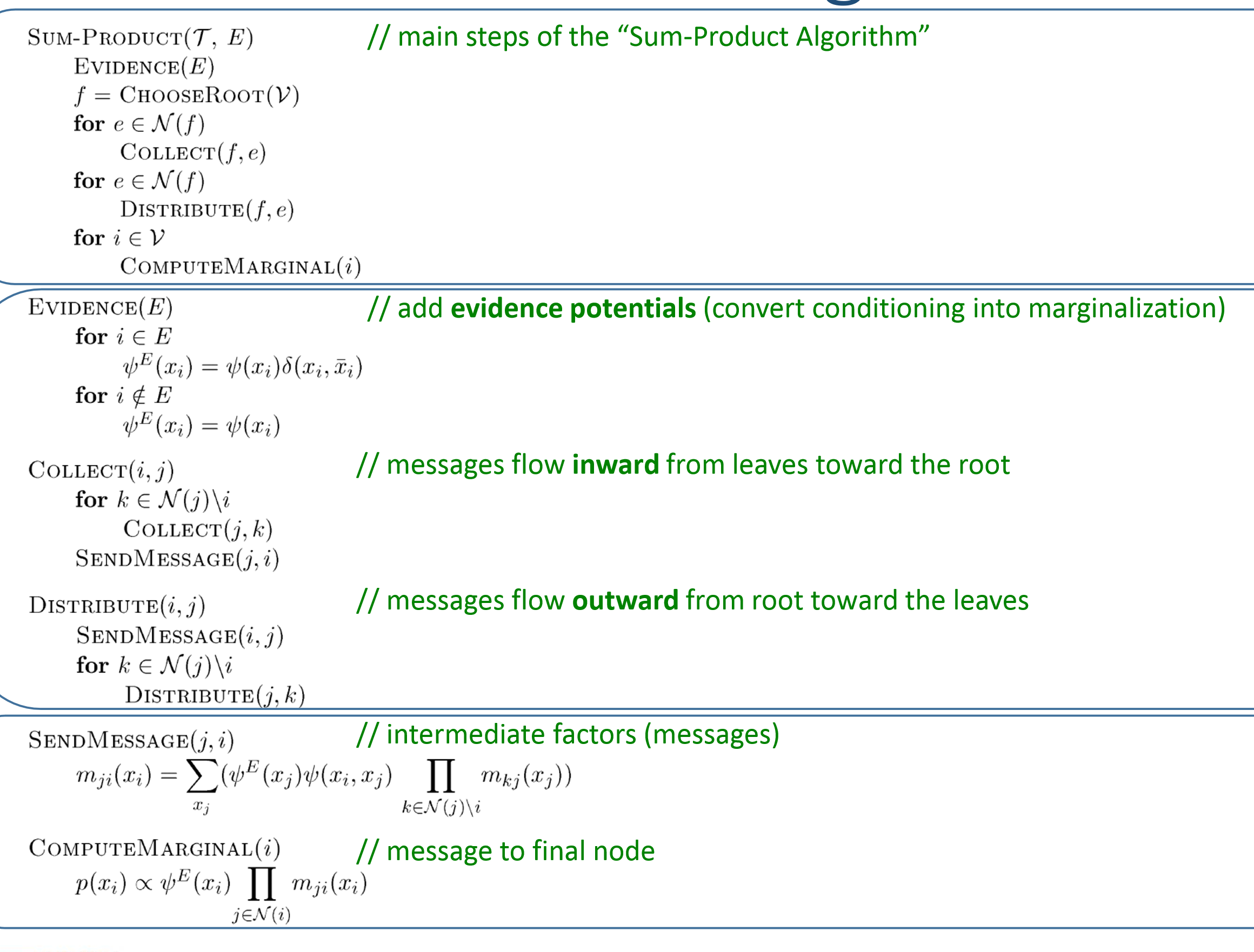
Sum-Product Algorithm (Belief Propagation Algorithm)

$ \checkmark$ All single-node marginals
$ \checkmark$ Tree like graphs (undirected tree without loop or can be moralized to such tree)
$ \checkmark$ Using one single run
$ \checkmark$ Cliques are single or pairs of nodes

Convert a directed tree to an undirected one

Define: $\psi(x_r) = p(x_r)$, $\psi(x_i.x_j)=p(x_j|x_i)$, $\psi(x_i)=1\quad\forall i\neq r$, Partition function $Z=1$.

Define local potetials

$\psi_i^E(x_i)=\begin{cases}\psi_i(x_i)\delta(x_i,\bar{x_i})\quad i\in E \\\psi_i(x_i)\qquad\qquad otherwise \end{cases}$ $p(x|\bar{x_E})=\frac{1}{Z^E}(\prod_{i\in V}\psi^E(x_i)\prod_{(i,j)\in E}\psi(x_i,x_j))$

Construct tree structure

Order: Depth-Fist Traversal.
Take query node $X_f$ as root.
Directing all edges pointing away from $X_f$.
Elimination proceeds inward from leaves with tree width equals to one.

Inward

Send message $(j,i)$:

$m_{ji}=\sum_{x_j}(\psi^E(x_j)\psi(x_i,x_j)\prod_{k\in N(j)- i}m_{kj})$

This message can be re-used.
Compute Marginal:

$p(x_f|\bar{x_E})\propto\psi^E(x_f)\prod_{e\in N(f)}m_{ef}$

which is the unnormalized conditional probability.

Message Passing Protocol: a node can send a message to a neihboring node if and only if it has received messages from all its other neighbors.

Two phase approval: inward & outward.
sum-product