Markov Random Fields (Undirected Graphical Models)

为什么需要无向图模型

使用无向图模型(UGM: Undirected Graphical Models) $\mathcal G(\mathcal V,\mathcal E)$来表示Markov Random Field(Markov network)。
$\mathcal V$ : 顶点集合，每个顶点与一个随机变量 $X_i$ 一一对应。
$\mathcal E$ : 无向边集合。
边没有方向性，这对于一些图像处理或空间分析问题更加自然。
For MRF, conditional independence is determined by simple graph separation, not the defination of “blocked”.

Conditional independence properties

Global Markov Property

对于点集A、B、C：$X_A\perp X_B|X_C$ 当且仅当：在图 $\mathcal G$ 中 集合C的点将A和B中的点隔离开，即：当移除所有C中点后，不存在A中点到B中点的路径。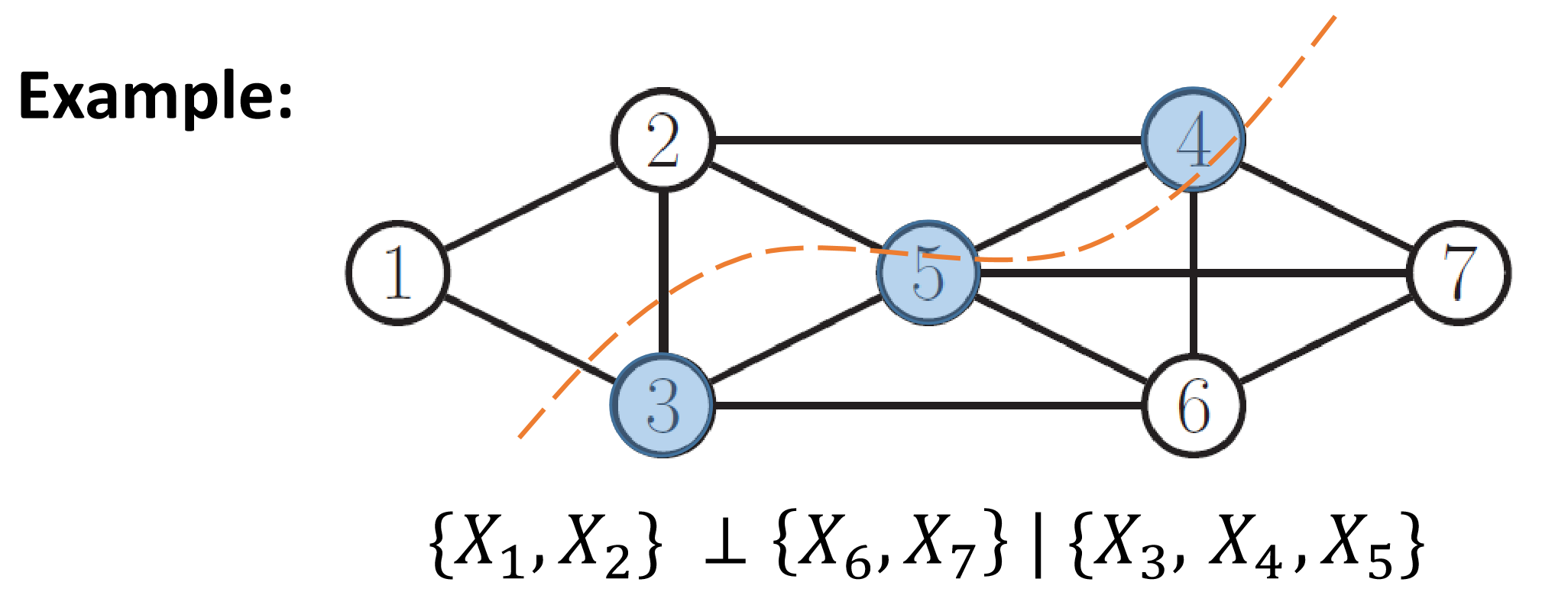

Local Markov Property

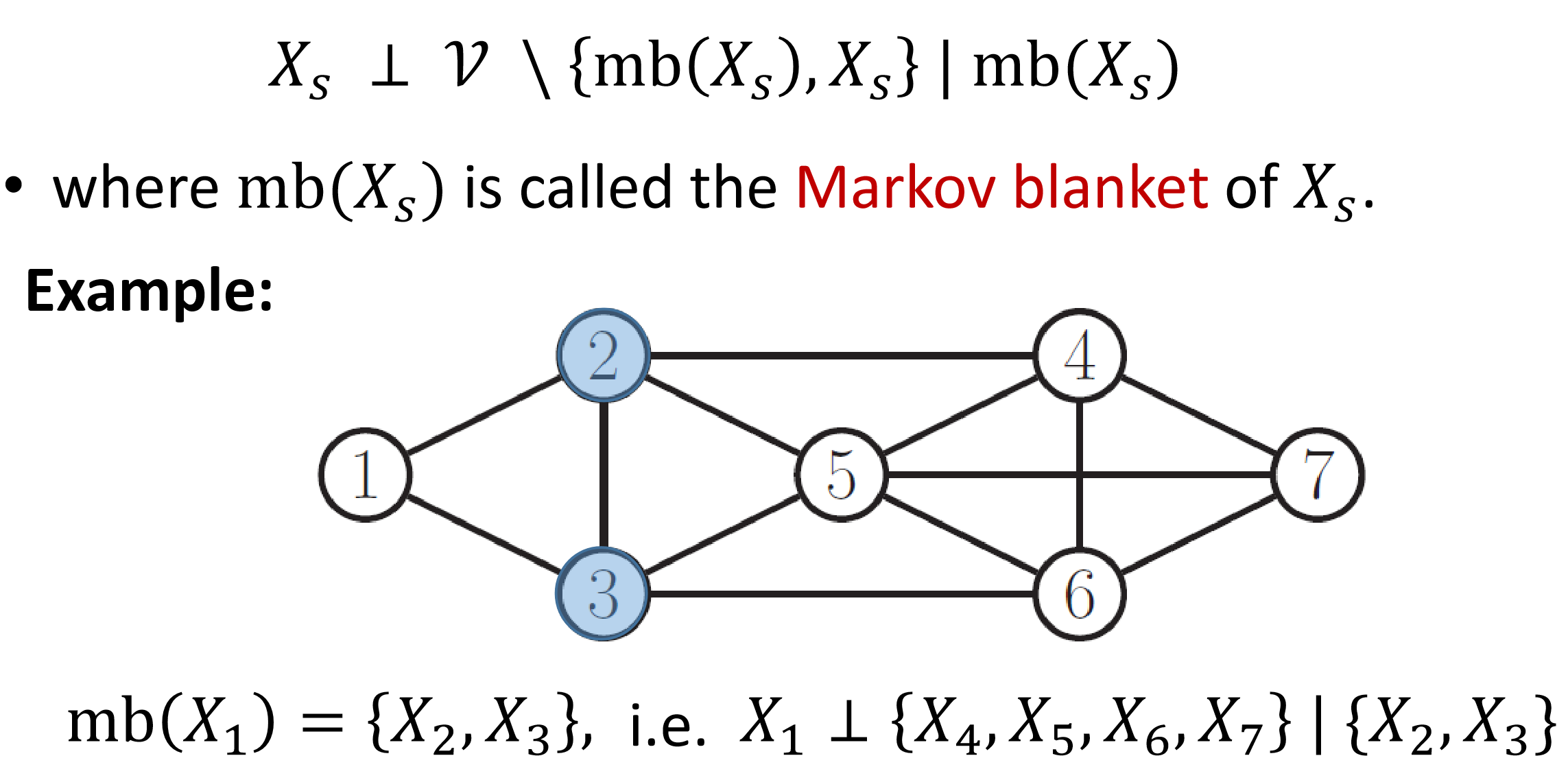
Pairwise Markov Property

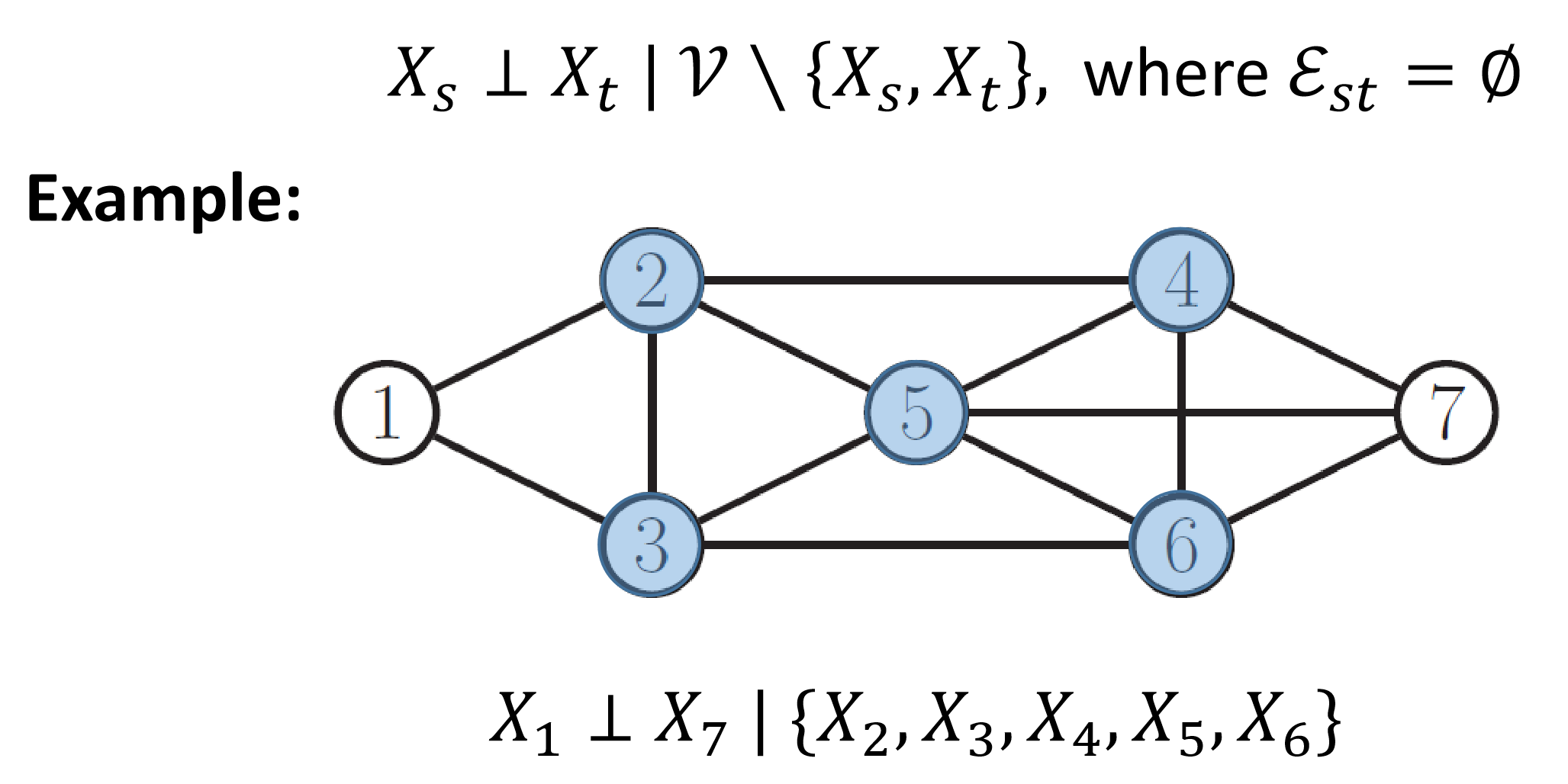
彼此等价

Global Markov implies local Markov which implies pairwise Markov.
Assuming p(x) > 0 for all x, pairwise Markov implies global Markov.

Independence-Map

The I-Map of a joint distribution $p(𝑥1,…,𝑥𝑁)$, often written as $𝐼(𝑝)$ represents all independencies in $p(𝑥1,…,𝑥𝑁)$.
Similarly, the I-Map of a directed/undirected graph $𝒢$, i.e. $\mathcal I(\mathcal G)$ represents all independencies encoded in $𝒢\mathcal G$.

Intersection Lemma

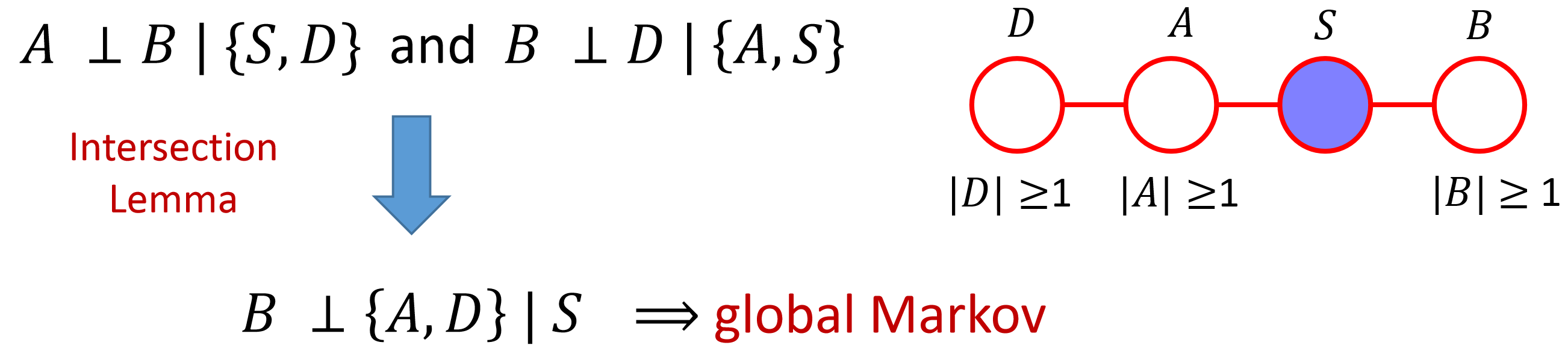
Comparative Semantics

Convert the DGM to a UGM by dropping the orientation of the edges is not always correct!

Parameterization of MRFs

For DGMs, we only need to focus on the local conditional probabilities of a node and its parents ( $p(x_i|x_{\pi_i})$ ), and the joint probability is a product of local conditional probabiities as a result of the chain rule:

$$p(x_1,...,x_N)=\prod_{i=1}^Np(x_i|x_{\pi_i})$$

Local parameterization is difficult for UGMs as there is no topological ordering associated with UGMs.

So we use functions to represent the local parameterization instead of the conditional distribution.

Recall two nodes $X_i$ and $X_j$ that are not linked directly, they are conditionally independent given all the other nodes. So we can place $X_i$ and $X_j$ in defferent dactors when obtaining a factorization of the joint probability.
This implies that we cannot have a local function that depends on both $X_i$ and $X_j$ in the parameterization.

Maximal Clique

If two nodes are linked, they must appeal in the same factor. So, all the nodes $X_C$ that belong to a maximal clique $C$ in the UGM appear together in a local function $\psi(x_C)$ . Conditional independence is impossible for any two nodes in maximal clique!

Hammersley-Clifford theorem:

$$p(y|\theta)=\frac{1}{Z(\theta)}\prod_{c\in \mathcal C}\psi_c(y_c|\theta_c)$$

$\mathcal C$ : the set of all the maximal cliques of $\mathcal G$
$\psi_c(.)$: the factor or potential function of clique c
$\theta$; the parameter of the factor $\psi_c(.)$ for $c\in\mathcal C$
$\psi_c(c|\theta_c)$ is not a conditional distribution but just an arbitrary chosen positive function:

$$Z(\theta)=\sum_y\prod_{c\in\mathcal C}\psi_c(y_c|\theta_c)$$

$Z(\theta)$: partition funtion, to ensure the overall distribution sums to 1

Parameterization of MRFs is not unique.

• define over maximal cliques
• pairwise parameterization
• define over all cliques, i.e., cannonical parameterization

Canonical Parameterization

Each node is viewed as a clique. In canonical parameterization we include all the possible cliques.
Uniform prior can be assumed on any potential function, i.e., set all potential function of edges to 1 (optional)

Gibbs Distribution

$$p(y|\theta)=\frac{1}{Z(\theta)}exp(-\sum_cE(y_c|\theta_c))$$

$E(y_c)>0$: energy associated with the variables in clique c as the potential function, using in particals’ random moving in air or liquid.
Convert Gibbs distibution to a UGM: (Energy based models)

$$\psi_c(y_c|\theta_c)=exp(-E(y_c|\theta_c))$$

High probability states correspond to low energy configurations.

Log-linear potential Functions

Define the log potentials as a linear function of the parameters $\theta_c\in\mathbb{R}^M$:

$$log\psi_c(y_c)=\phi_c(y_c)^T\theta_c$$

$\phi_c$: feature vector derived from values of variables $y_c$

$$logp(y|\theta)=\sum_c\phi_c(y_c)^T\theta_c-logZ(\theta)$$

also known as a maximum entropy or a log-linear model.
If $M=|C|=3$, we only need 3 parameter $\theta_c=[\theta_{c1},\theta_{c2},\theta_{c3}]$ instead of $2^3$ parameters.

Combine UGM and DGM

A DGM can be converted into a UGM by joining all the links among parents for a head-to-head node, i.e. moralization
This process preserves the joint distribution but conditional independence is lost.

Discriminative vs Generative Models

Discriminative models: model the posterior directly $p(\mathcal C_k|x)$
eg. logistic regression model

Generative models: sampling from the distribution is possible to generate synthetic data points in the input space.
Likelihood: $p(x|\mathcal C_kx)$

Conditional Random Field(CRF)

A CRF or discriminative random field is a version of an MRF where all clique potentials are conditioned on global input x:

$$p(y|x,w)=\frac{1}{Z(x,w)}\prod_c\psi_c(y_c|x,w)$$

log-linear representation:

$$\psi_c(y_c|x,w)=exp(w_c^T\phi(x,y_c))$$

CRF make use of input data and the predictions can be data-dependent, but require labeled training data and learning is slower.