Multilayer Perceptron (MLP)
The Perception
input: $x_1,x_2…,x_N$
weight: $w_1,w_2,…,w_N$
output: $y={\mathcal g }(\boldsymbol{w^Tx})=\begin{cases} 1,\qquad if\quad\boldsymbol{w^Tx}>0 \\ 0,\qquad else\end{cases}$
Linear functions are limited: Linear models cannot fit in data from XOR function:
| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- sign function: $y={\mathcal g }(x)=\begin{cases} 1,\qquad if\quad x>0 \\ 0,\qquad else\end{cases}$
Non-Linear feature transformations
$\boldsymbol{h}=\mathbf{W}\boldsymbol{x}+\boldsymbol{c}$, $\mathbf{W}\in R^{2\times 2}$, $\boldsymbol{c}\in R^2$
$\\\mathbf{W}=\begin{pmatrix}1\quad 1\\1\quad 1\end{pmatrix}\qquad \boldsymbol{c}=\begin{pmatrix}0\\ -1\end{pmatrix}$
| $x_1$ | $x_2$ | $\boldsymbol{x}$ | $\mathbf{W}\boldsymbol{x}+\boldsymbol{c}$ | $\boldsymbol{h}$ | $h_1$ | $h_2$ | $y$ |
|---|---|---|---|---|---|---|---|
| 0 | 0 | $\begin{pmatrix}0\\0\end{pmatrix}$ | $\begin{pmatrix}0\\ -1\end{pmatrix}$ | $\begin{pmatrix}0\\0\end{pmatrix}$ | 0 | 0 | 0 |
| 0 | 1 | $\begin{pmatrix}0\\1\end{pmatrix}$ | $\begin{pmatrix}1\\0\end{pmatrix}$ | $\begin{pmatrix}1\\0\end{pmatrix}$ | 1 | 0 | 1 |
| 1 | 0 | $\begin{pmatrix}1\\0\end{pmatrix}$ | $\begin{pmatrix}1\\0\end{pmatrix}$ | $\begin{pmatrix}1\\0\end{pmatrix}$ | 1 | 0 | 1 |
| 1 | 1 | $\begin{pmatrix}1\\1\end{pmatrix}$ | $\begin{pmatrix}2\\1\end{pmatrix}$ | $\begin{pmatrix}2\\1\end{pmatrix}$ | 2 | 1 | 0 |
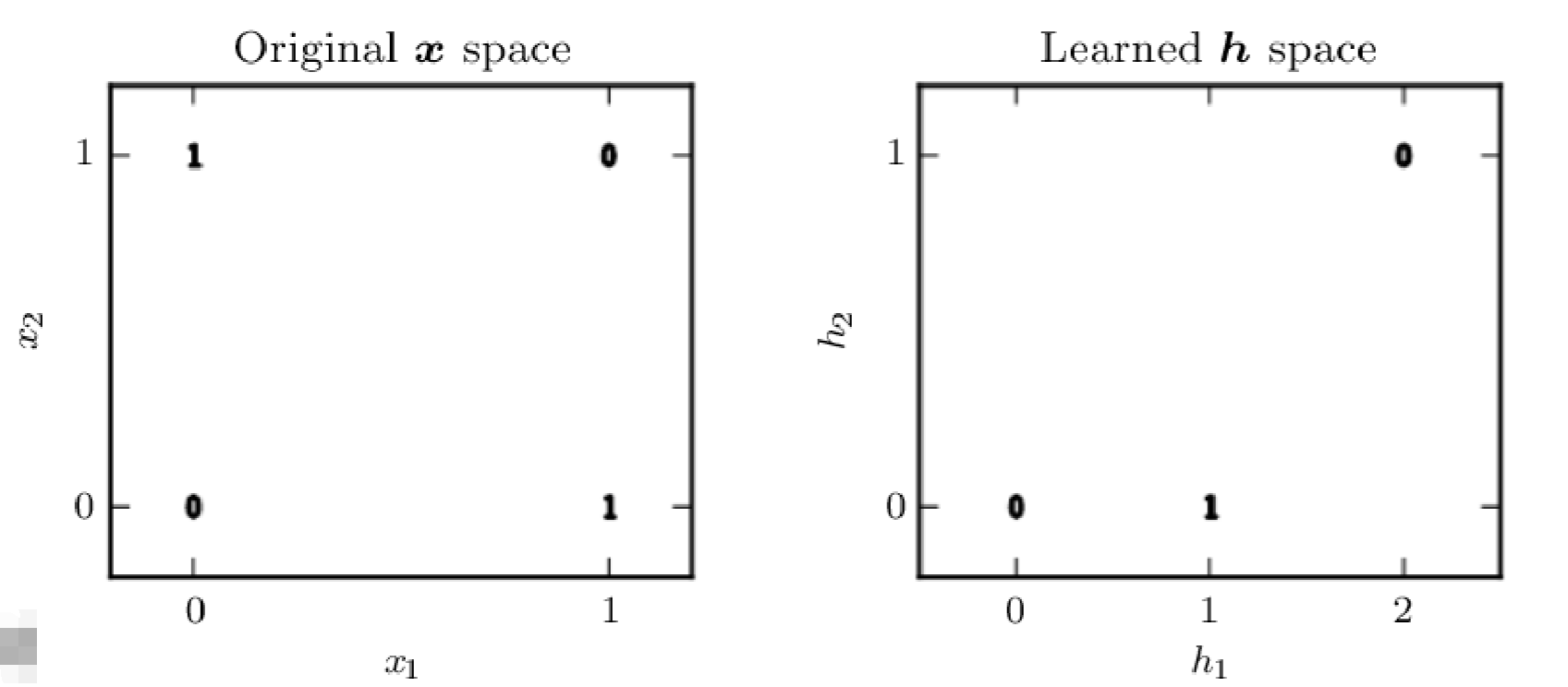
In this case, there exist a linear function that can fit in $h_1,h_2,y$:
$\widetilde{y}=\boldsymbol{h^Tw}+b,\boldsymbol{w}\in R^2,b\in R\\\boldsymbol{w}=\begin{pmatrix}1\\ -2\end{pmatrix},b=0$
Rectified Linear Unit, ReLU: ${\displaystyle f(x)=\max(0,x)}$
$max(\begin{pmatrix}0\\0\end{pmatrix},\begin{pmatrix}1\\ -1\end{pmatrix})=\begin{pmatrix}1\\0\end{pmatrix}$
Multilayer Perceptron
In perceptron, there are at least one non-linear hidden layer
$i^{th}$ layer consists of a linear/affine transformation function:
A linear function is always followed by a non-linear function $g()$:
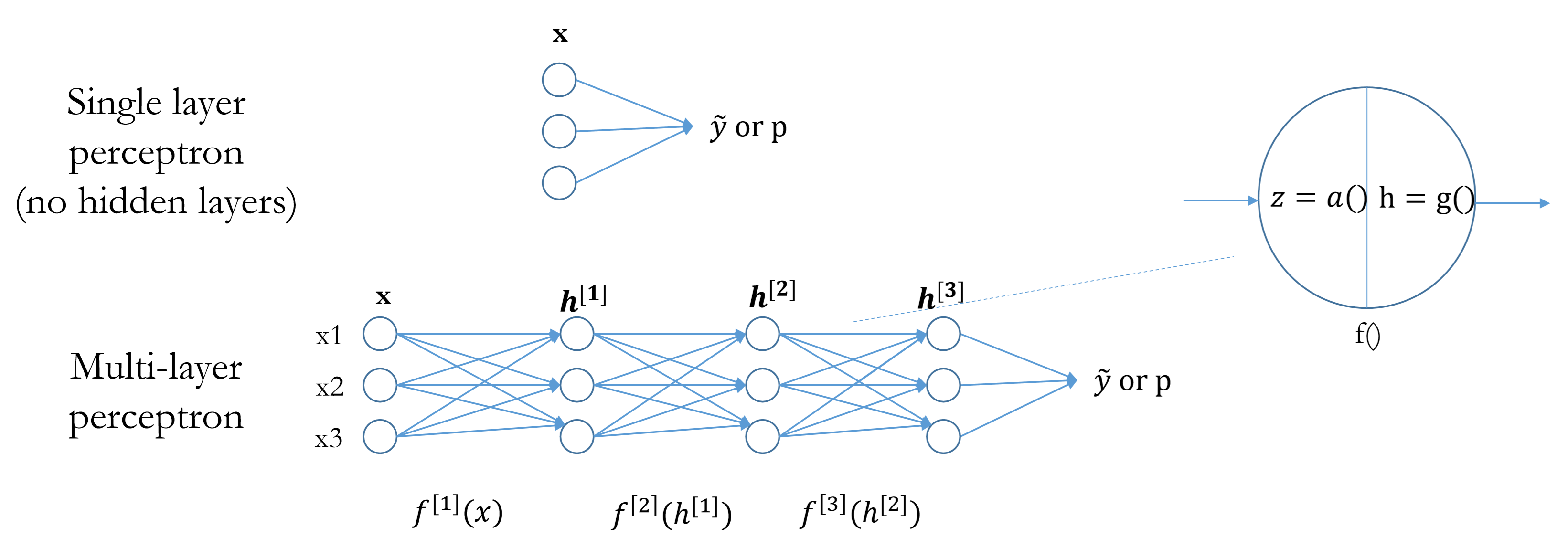
If one linear function is directly connected to another linear function, the two functions can be combined to one single linear function, i.e. succesive linear transformations together form another linear transformation.
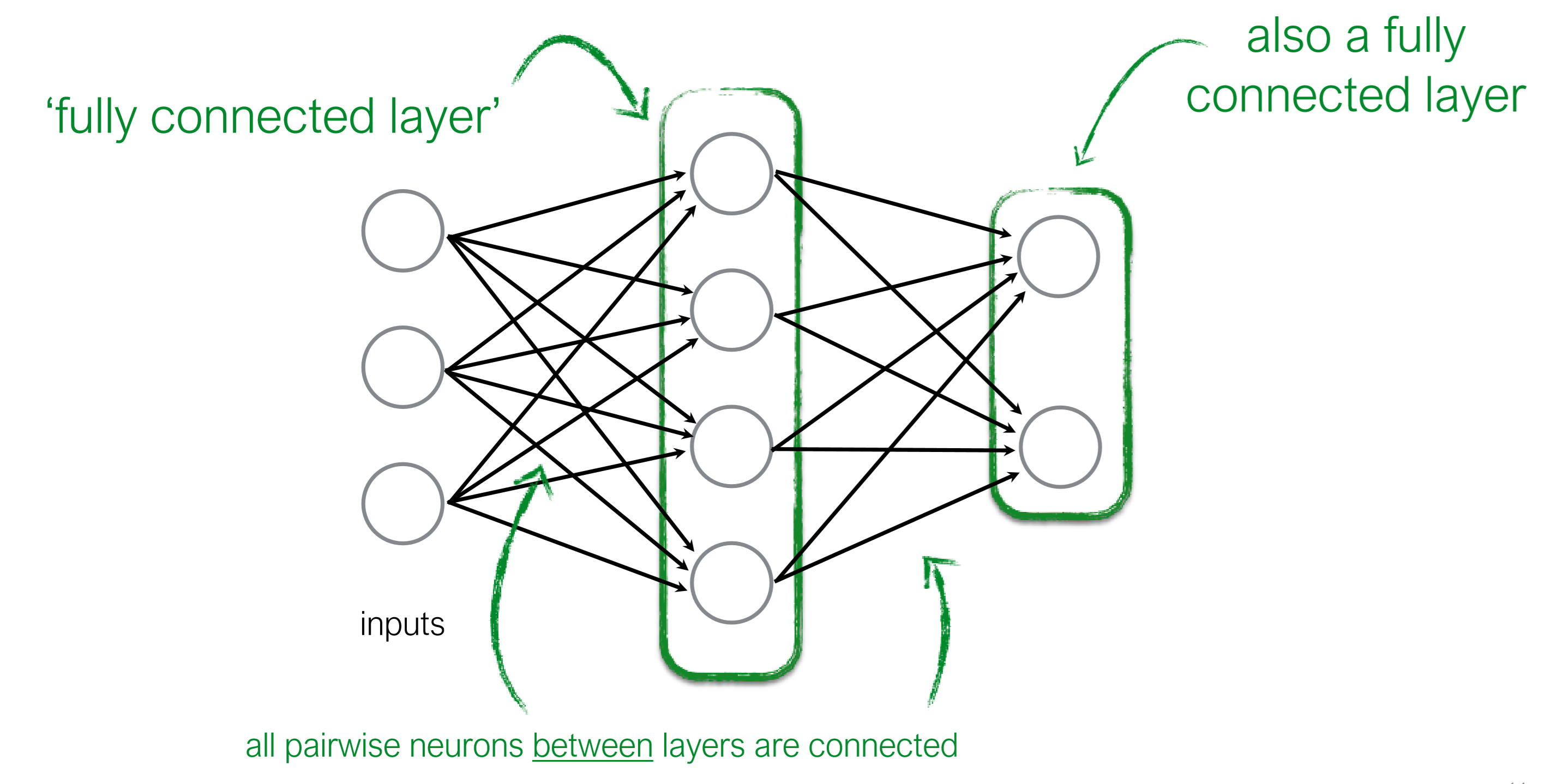
number of neurons(perceptrons): 4 + 2 = 6
number of weights(edges): (3 * 4) + (4 * 2) = 20
number of parameters total: 20 + (4 + 2) = 26 (weight_num + bias_num)
Activate Function $g()$

Training MLP
for classification: Cross-entropy loss
for regression: L2(Squared Euclidean distancess)
GD algorithm:
- compute average loss $J$
- computer gradient for each parameter
- update every parameter according to their gradients

Backpropagation
