条件独立 conditional independence

例如：一个人的基因与父母之外的非后代的基因在给定其父母基因的条件下相互独立：

$X_{child}\perp (X_{non-descendants}\backslash X_{parent}) | X_{parent}$

Markov假设：任意节点在局部仅仅依赖于它的直接父节点

贝叶斯网络 Bayes Network

定义 Definition

使用有向无环图(DAG: directed acyclic graph)$\mathcal G(\mathcal V,\mathcal E)$来表示条件独立，其中 $\mathcal V$ 是顶点集合，$\mathcal E$ 是有向边集合。每个顶点代表一个随机变量，有向边代表随机变量之间的依赖关系。

Ancestors：前序结点
Descendants：后续结点

$X_{\pi_i}$是随机变量 $X_i$ 的parent
如果$X_i$入度为0，则parent为空集

必须是无环图，即：图中必须存在拓扑排序(“There exists an ordering of the nodes such that there are no links that go from any node to any lower numbered node. “)
For practical applications of probabilistic models, it will typically be the highernumbered variables corresponding to terminal nodes of the graph that represent the observations, with lower-numbered nodes corresponding to latent variables.
The hidden variables in a probabilistic model need not, however, have any explicit physical interpretation but may be introduced simply to allow a more complex joint distribution to be constructed from simpler components.

Markov Assumption

$X_i\perp (X_{nonDesc(X_i)})\backslash X_{\pi_i})|X_{\pi_i}$

这种parent-child模型代表了条件独立：$p(x_i|X_{\pi_i})$

联合概率 Joint Probability

“ The joint distribution deﬁned by a graph is given by the product, over all of the nodes of the graph, of a conditional distribution for each node conditioned on the variables corresponding to the parents of that node in the graph”
随机变量的联合概率可以从图中表示为所有局部条件独立的乘积：（假设$x_1,…x_N$是拓扑排序）

$p(x_1,...x_N)=\prod_{i=1}^Np(x_i|x_{\pi_i})$

This key equation expresses the factorization properties of the joint distribution for a directed graphical model.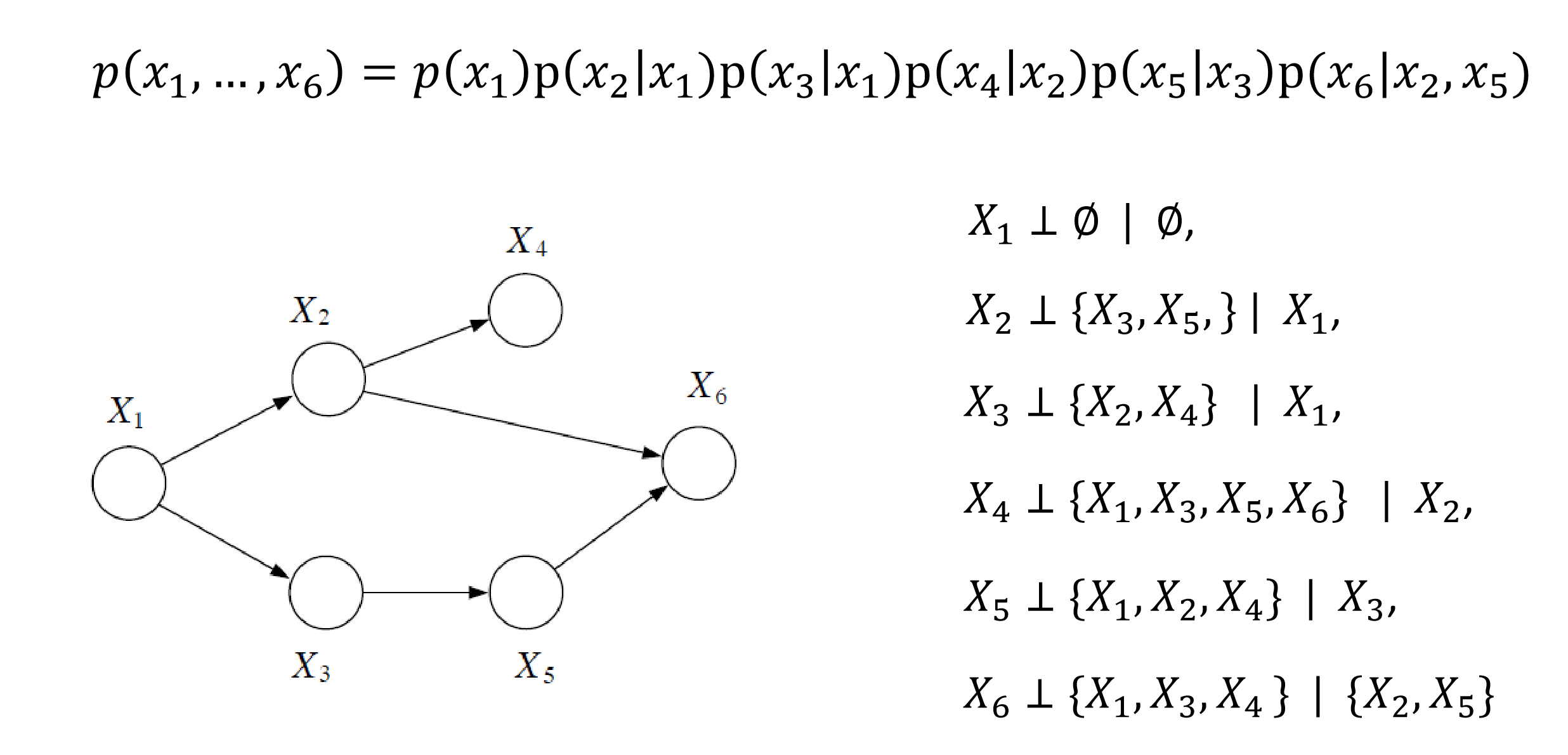
Markov_Assumption
要证明 $X_1$ 和 $X_3$ 在给定 $X_2$ 的情况下与 $X_4$ 独立，即证：$p(x_4|x_1,x_2,x_3)=p(x_4|x_2)$，可以分别求出 $p(x_1,x_2,x_3,x_4)$ 和 $p(x_1,x_2,x_3)$，两者相除得到 $p(x_4|x_1,x_2,x_3)$

Parameter Reduction

$m_i$ 是点 $X_i$ 的直接parent结点的个数，$K$ 是每个点可取值的个数。
$X_i$ 的条件概率可以用 $K^{(m_i+1)}$ 个参数来表示。
参数个数从 $K^N$ 减少到了 $K^{(m_i+1)}$，其中 $m_i << N$。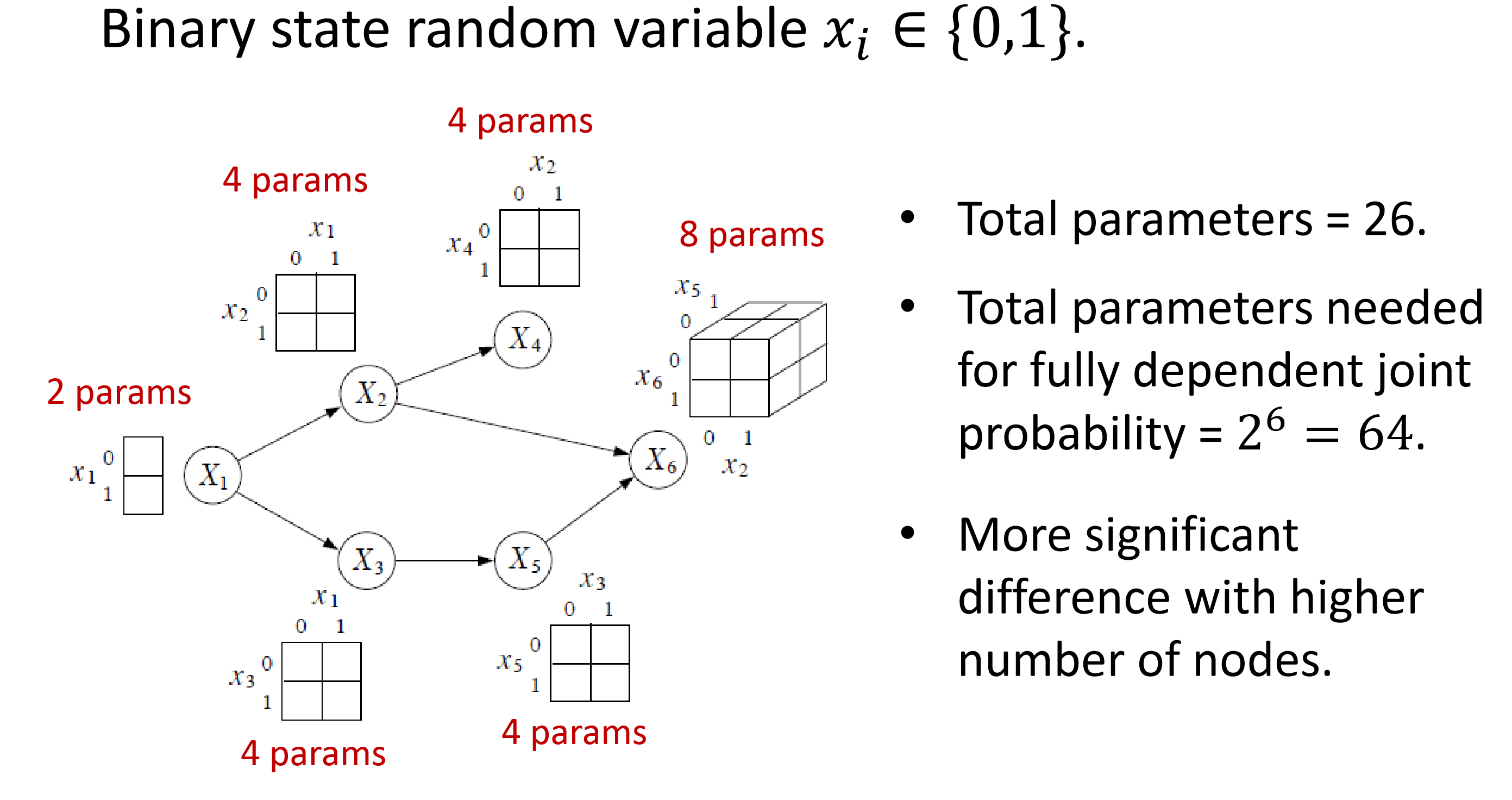
history

其它条件独立

除了parent-child产生的条件独立，图中也有其它的条件独立。如：$X_1\perp X_6| \{X_2,X_3\}$
直观解释：图中 $X_2,X_3$ 这两个点阻隔了(block)所有从 $X_1$ 到 $X_6$ 的路径
这暗示了图的分隔可以导向相对独立的产生。

Three Canonical 3-Node Graphs

顶点 $C$ 被称作 “head-to-tail” w.r.t $A$ 到 $B$ 的路径，这个顶点隔开了 $A$ 和 $B$ 并且成为了他们相互独立的条件。即：给定当前状态的情况下过去状态和未来状态相互独立。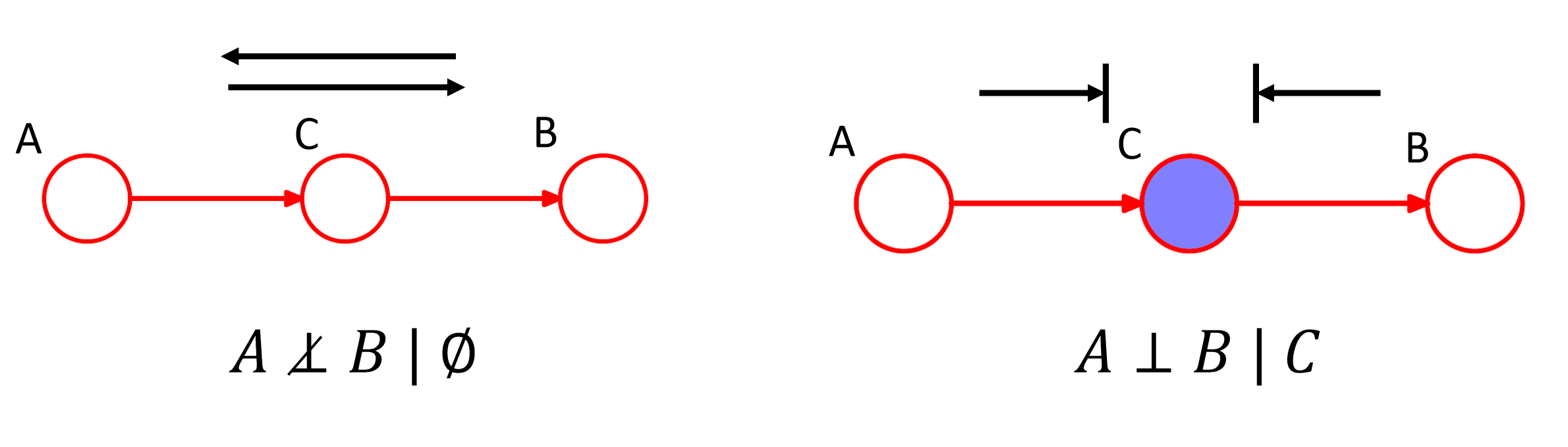
history

顶点 $C$ 被称作 “tail-to-tail” w.r.t $A$ 到 $B$ 的路径，这个顶点隔开了 $A$ 和 $B$ 并且成为了他们相互独立的条件。即：$C$ 解释了 $A$ 和 $B$ 之间所有的关联性。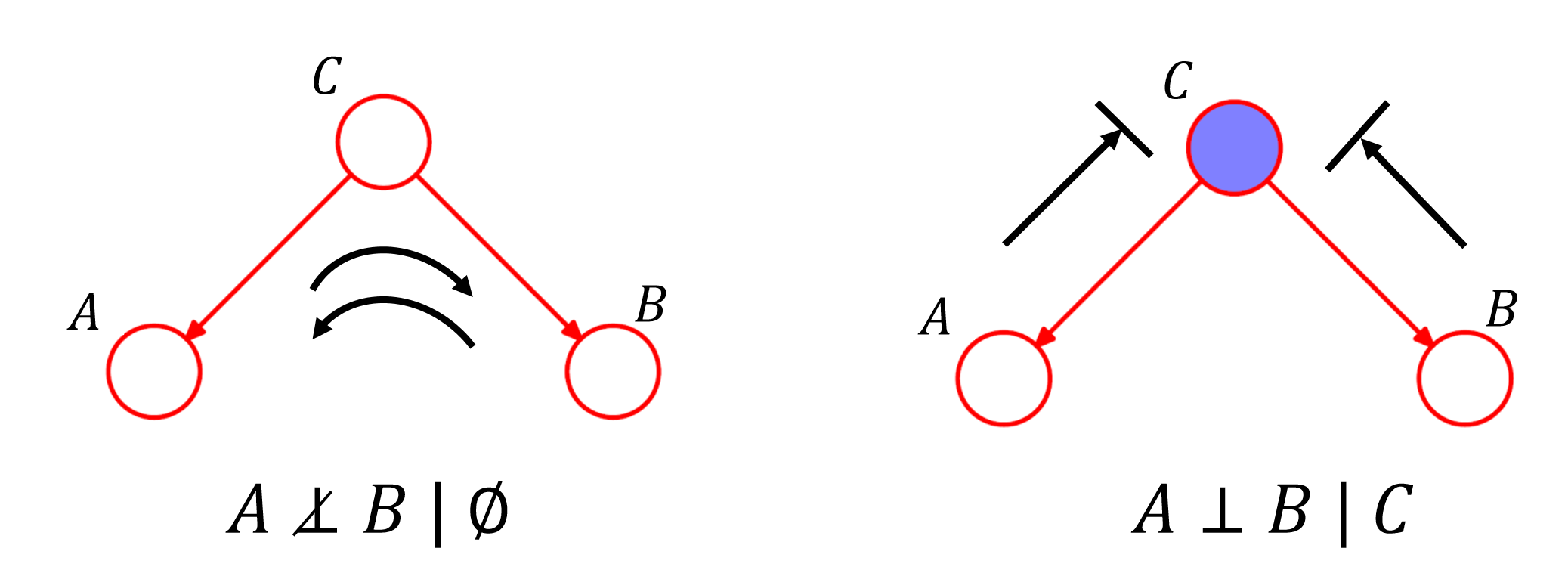
3-Node-Graph

顶点 $C$ 被称作 “head-to-head” w.r.t $A$ 到 $B$ 的路径，也称作”V-structure”。当 $C$ 不存在时，$A$ 和 $B$ 之间路径被阻隔，$A$ 和 $B$ 相互独立。而将 $C$ 当作条件时，连通了这条路径，导致存在了关联性(explaining-away effect)。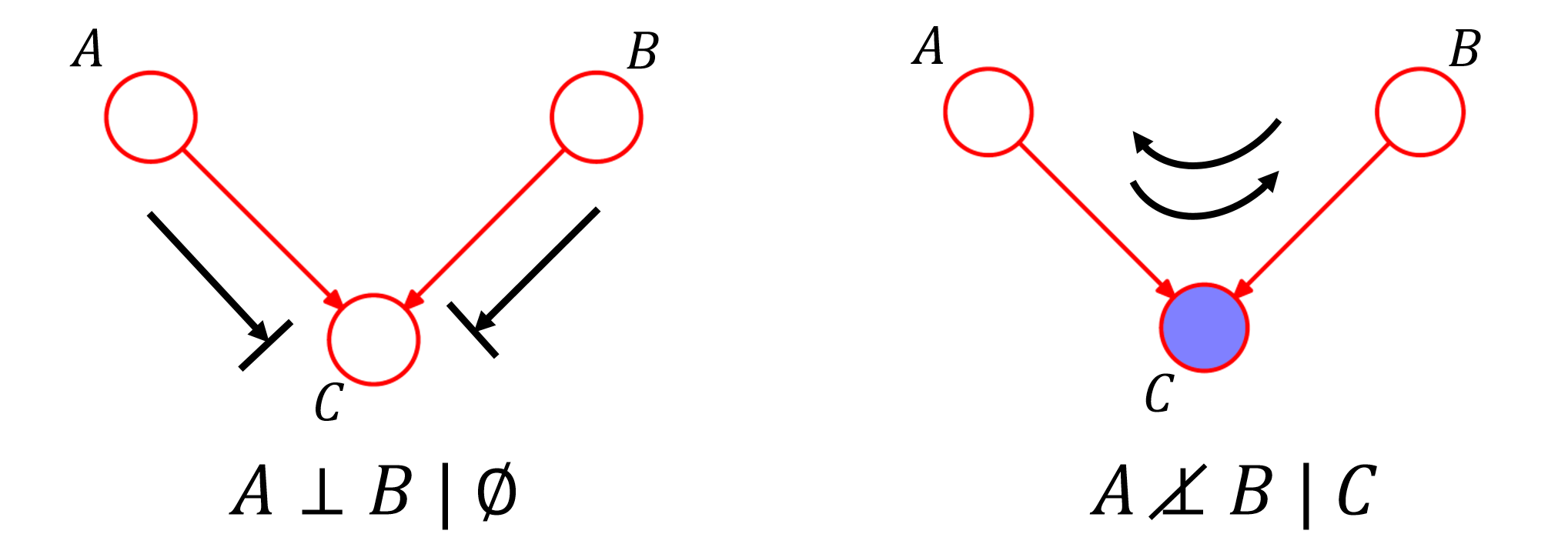
3-Node-Graph
$C$ 的每个子节点也都提供了这种连通性。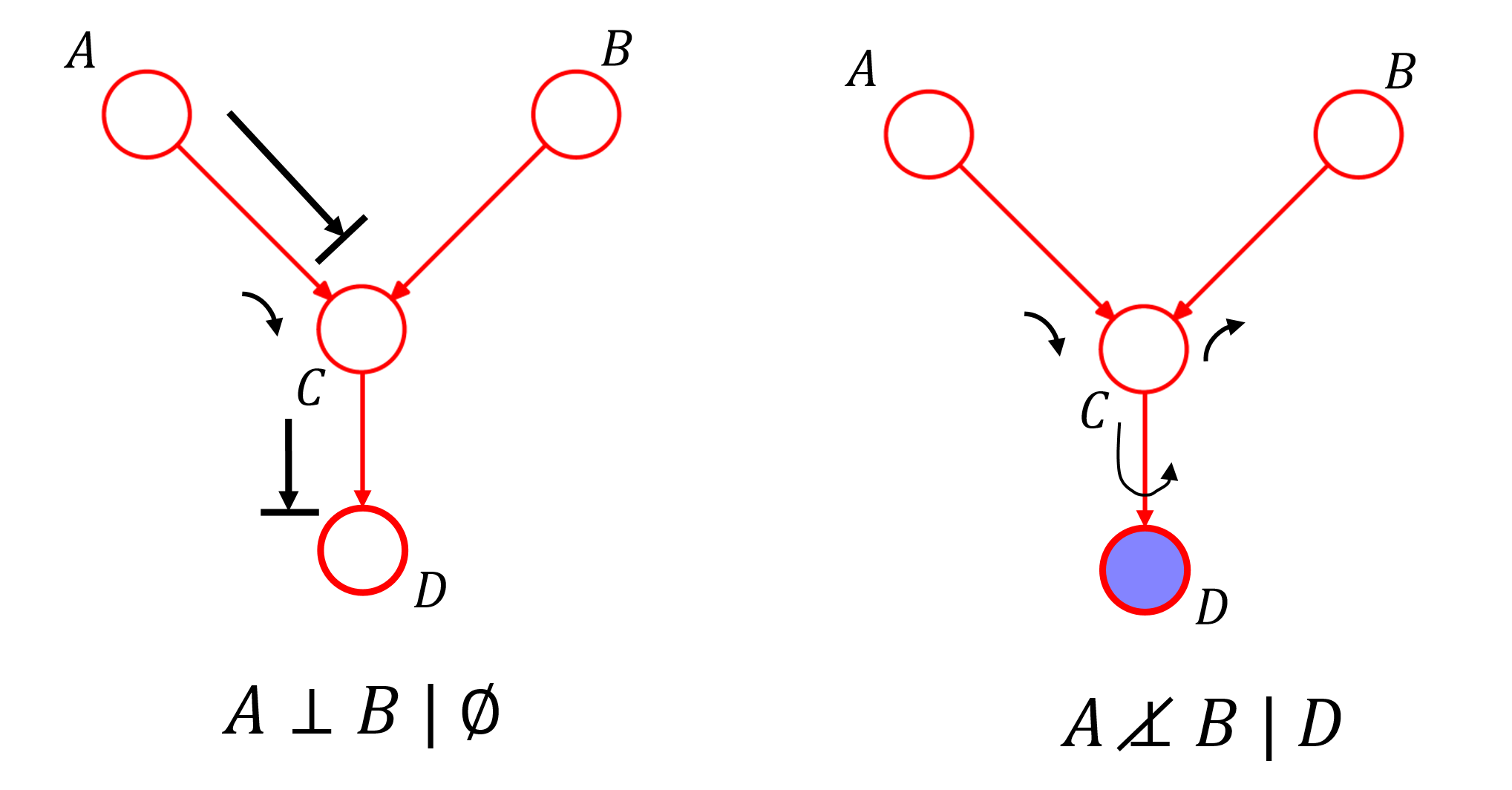

In summary, a tail-to-tail node or a head-to-tail node leaves a path unblocked unless it is observed in which case it blocks the path. By contrast, a head-to-head node blocks a path if it is unobserved, but once the node, and/or at least one of its descendants, is observed the path becomes unblocked.

Graph Separation (directional-seperated)

如果所有从点集$A$到点集$B$的路径都在点集$C$被观察到时被阻隔了(blocked)，那么 $A\perp B|C$。
$A$ is d-separated from $B$ by $C$.
Any such path is said to be blocked if it includes a node such that either

the arrows on the path meet either head-to-tail or tail-to-tail at the node, and the node is in the set C, or
the arrows meet head-to-head at the node, and neither the node, nor any of its descendants, is in the set C.

Bayes Ball Algorithm

是一个可达性算法，可以用BFS完成。
将点集$A$中的每个点上放置一个球，沿着路径进行滚动，如果被$C$阻隔则停住。
如果$A$中每个球都最终无法到达$B$中的点，则说明 $A\perp B|C$ ，否则$A$和$B$在给定$C$时不满足条件独立。

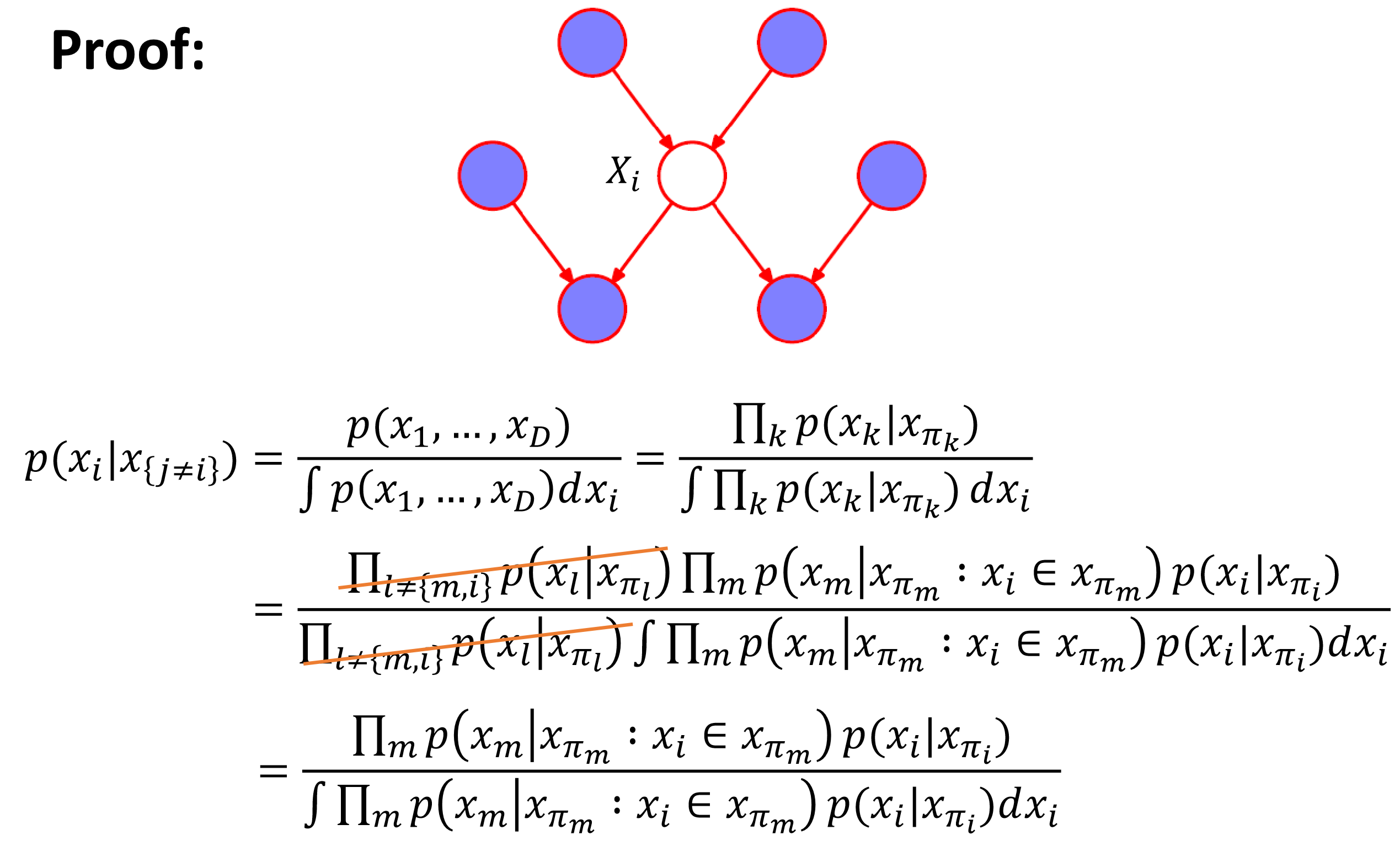
Markov Blanket

一个顶点 $X_i$ 仅依赖于自己的直接父节点(parent) $X_{\pi_i}$、直接子节点(child)和子节点的其它父节点(co-parent)。
$p(x_m|x_{\pi_m}:x_i\in x_{\pi_m})$ ：代表了顶点 $X_i$ 的直接子节点与它的直接父节点( $X_i$ 和它的co-parent)之间的依赖关系。
history