Linear Regression

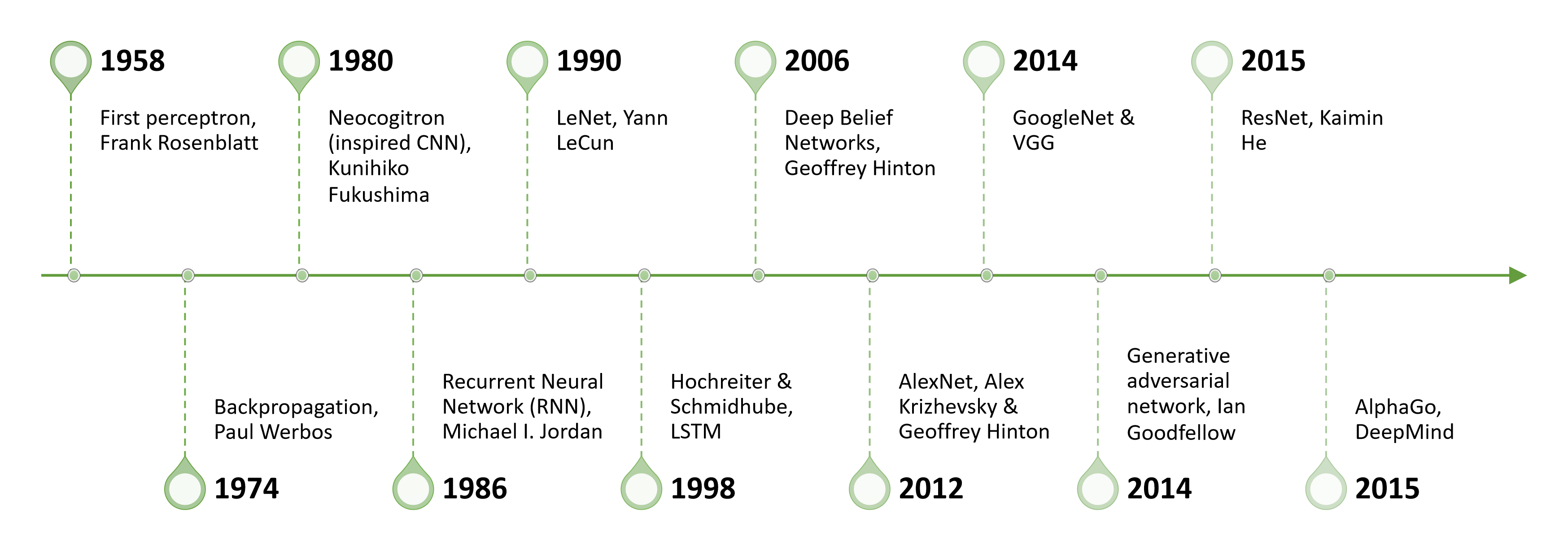
神经网络发展历程

神经网络主要依赖于特征转换(feature transformation)，通过准备数据、提取特征来构造模型。

神经网络中需要非线性处理单元(nonlinear processing unit)用来产生非线性边界(boundary)，以处理线性不可分的数据(dataset)。
CV的主要任务有：图像分类，实体识别，场景识别，图像生成。
NLP的主要任务有：问答系统，机器翻译
Speech：对话识别

单变量线性回归

线性回归(linear regression)解决的是一个回归任务，即：给定若干实例$(x,y)$，需要求得一个系统，以$x_i$为输入，输出对$y_i$的预测值$\widetilde{y_i}$。
在单变量线性回归中，$x_i$、$y_i$、$\widetilde{y_i}$都是标量(scalar)，该系统输出的$\widetilde{y_i}$是$x_i$的线性函数：$\widetilde{y_i}=w*x_i+b$。
使用损失函数(loss function)来衡量$w$、$b$对模型的模拟能力。损失函数值越小，拟合效果越好。
数据集$S_{train}=\{x^{(i)}，y^{(i)}\}, i = 1…m,|S_{train}|=m$
在参数 $w, b$ 的条件下的常用损失函数可以表示为：

• ${\mathcal L}1：L(x,y|w,b)=|\widetilde{y} - y|$
• ${\mathcal L}2：L(x,y|w,b)=\frac{1}{2}||\widetilde{y} - y||^2=\frac{1}{2}(\widetilde{y} - y)^2$
  选择 ${\mathcal L}2$ 因为它可微(differentiable)，更易进行优化和训练；系数$\frac{1}{2}$是为了让导数形式更简单。

定义training objective（此处使用平均误差）：$J(w,b)=\frac{1}{m}\sum_{i=1}^{m}{\mathcal L}(x_i,y_i|w,b)$
累加：获得全局(overall)信息以达到全局优化
平均：消除数据集大小对loss值的影响

优化和训练过程：

$$\min_{w,b}J(w,b)$$ $$\to\min_{w,b}\frac{1}{m}\sum_{i=1}^{m}{\mathcal L}(x_i,y_i|w,b)$$ $$\to \min_{w,b}\frac{1}{2m}\sum_{i=1}^{m}(w*x_i+b - y_i)^2$$

当$w,b$不收敛（固定更新轮数or设定阈值判断收敛）时，重复以下步骤：

• 固定b，学习w $$\min_{w}\frac{1}{2m}\sum_{i=1}^{m}(w*x_i+b - y_i)^2$$ $$\to \min_wC_1w^2+C_2w+C_3$$ 由于b被固定了，w前的系数$C_1,C_2$和后面的偏置$C_3$都是常数(constant)。此时优化函数是一个关于w的一元二次函数，很容易求解当该函数J取得最小值时$w = -\frac{C_2}{2C_1}$。
  当优化函数复杂时可以通过梯度下降作为优化函数进行求解：$w=w-\alpha\frac{\partial J}{\partial w}$
• 固定w，学习b
  b的学习过程与w类似，将w看作常量，优化函数转换为关于b的一元二次函数，将这个函数通过优化函数（如梯度下降等）求解最优处的b值。

多变量线性回归

将一个实例$\boldsymbol{x}$的n个特征表示为一个$n\times 1$大小的列向量，其中$x_i$代表实例x的第i个特征，每个实例x对应一个目标值y。待学习的权重w是一个向量，$w_i$代表了特征$x_i$的重要程度。
即：单一实例$\boldsymbol{x}=\begin{pmatrix} x_1 \\ x_2 \\ … \\ x_n\\\end{pmatrix}$
建立线性回归模型（将输入映射到输出）：

$$\begin{aligned} \widetilde{y}=\boldsymbol{w^Tx}+b &=\sum_{i=1}^{n}w_ix_i+b\\ &=\begin{pmatrix} w_1,w_2...w_n\end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ ... \\ x_n\\\end{pmatrix} + b\\\\ &= \begin{pmatrix} w_1,w_2...w_n, b\end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ ... \\ x_n\\1\end{pmatrix}\\ \to \widetilde{y}=\bar w^T\bar x \end{aligned}$$

对于单一实例求梯度：

$$J(w)=\frac{1}{2}||\widetilde{y} - y||^2=\frac{1}{2}( \boldsymbol{w^Tx}-y)^2$$ $$\frac{\partial J(\boldsymbol{w})}{\partial \boldsymbol{w}}=(\boldsymbol{w^Tx}-y)\boldsymbol{x}$$

我们可以选择对每个实例$x^{(i)}$，$y^{(i)}$分别求loss值并累加求平均，再对每个实例的梯度求累加，但这样对实例逐个操作的效率不如将所有实例合并视为矩阵再进行矩阵操作代表效率高。
将每个特征向量实例(列向量)通过转置放在矩阵的一行：

$$\mathbf{X} = \begin{pmatrix} {\boldsymbol{x^{(1)}}}^T \\ {\boldsymbol{x^{(2)}}}^T \\ ... \\ {\boldsymbol{x^{(m)}}}^T\end{pmatrix} \qquad \boldsymbol{y} = \begin{pmatrix} {y^{(1)}}^T \\ {y^{(2)}}^T \\ ... \\ {y^{(m)}}^T\end{pmatrix} \qquad \boldsymbol{\widetilde{y}}=\mathbf{X}\boldsymbol{w}$$ $$J(\boldsymbol{w})=\frac{1}{2m}||\widetilde{\boldsymbol{y}} - \boldsymbol{y}||^2=\frac{1}{2m}(\widetilde{\boldsymbol{y}} - \boldsymbol{y})^T(\widetilde{\boldsymbol{y}} - \boldsymbol{y})\qquad \boldsymbol{u}=\widetilde{\boldsymbol{y}} - \boldsymbol{y}$$

由于：

$$\frac{\partial(u(x)\cdot v(x))}{\partial x} = \frac{\partial u^Tv}{\partial x} = \frac{\partial u}{\partial x}\cdot v+\frac{\partial v}{\partial x}\cdot u$$ $$\frac{\partial {\boldsymbol{u}}}{\partial {\boldsymbol{w}}} = {\mathbf{X}}^T$$

可以得到：

$$\frac{\partial J(\boldsymbol{w})}{\partial \boldsymbol{w}}=\frac{1}{2m}(\frac{\partial {\boldsymbol{u}}}{\partial {\boldsymbol{w}}}\cdot {\boldsymbol{u}} + \frac{\partial {\boldsymbol{u}}}{\partial {\boldsymbol{w}}}\cdot {\boldsymbol{u}})=\frac{1}{m}{\mathbf{X}}^T{\boldsymbol{u}}=\frac{1}{m}{\mathbf{X}}^T(\widetilde{\boldsymbol{y}} - \boldsymbol{y})$$

显然在当前条件下导数取0时损失函数$J(w)$值最小，此时令$\frac{\partial J(w)}{\partial w}=0$有：

$${\mathbf{X}}^T({\mathbf{X}}{\boldsymbol{w}}-{\boldsymbol{y}})=0$$ $$\to {\mathbf{X}}^T{\mathbf{X}}{\boldsymbol{w}}={\mathbf{X}}^T{\boldsymbol{y}}$$ $$\to {\boldsymbol{w}}=({\mathbf{X}}^T{\mathbf{X}})^{-1}{\mathbf{X}}^T{\boldsymbol{y}}$$

同样也可以使用梯度下降进行训练：${\boldsymbol{w}}={\boldsymbol{w}}-\alpha\frac{\partial J({\boldsymbol{w}})}{\partial {\boldsymbol{w}}}$

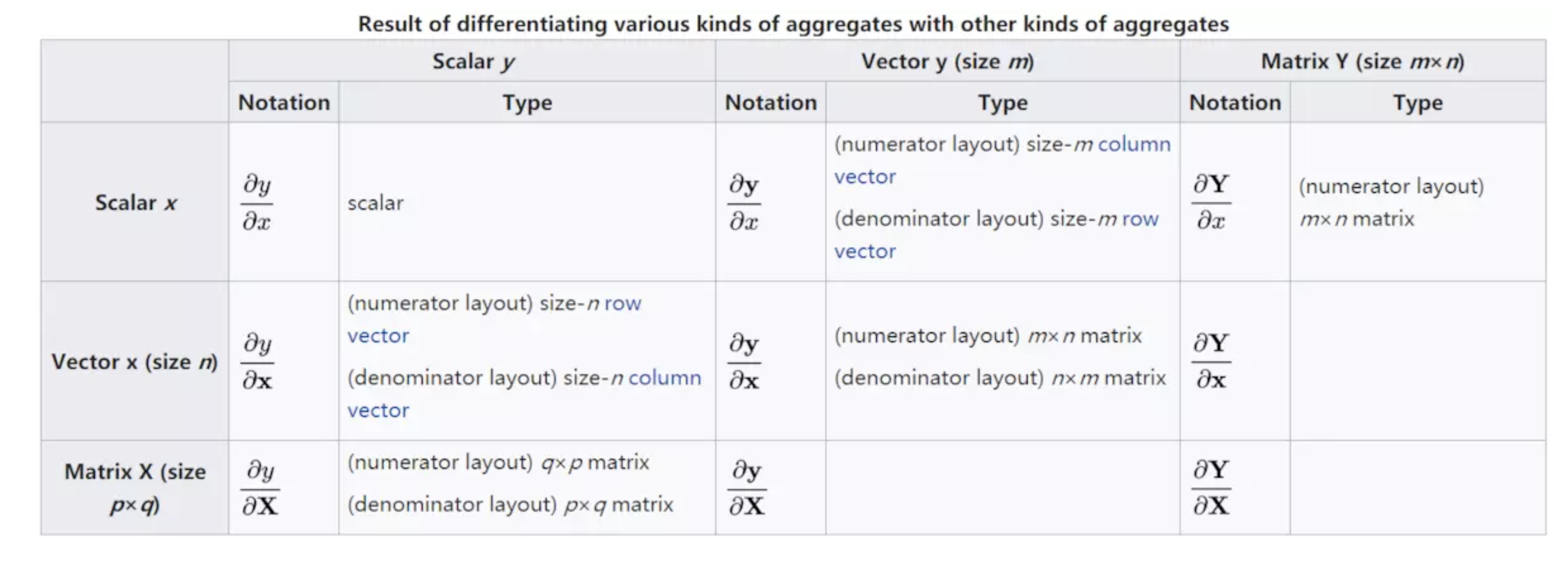
• w.r.t.: with respect to

• 分母布局(denominator layout)：求导结果的维度以分母为主，即结果的第一维度与分母相同。分子布局和分母布局的结果是互为转置的关系。

  https://en.wikipedia.org/wiki/Matrix_calculus#cite_note-2
  

• Pipeline of ML: Dataset, modeling, optimization, validation and inference

• 使用 $L$ 来表示单一实例上的损失值
  使用 $J$ 来表示实例集合上的平均损失值

• np.multiply()函数 等价于 星号（*）：每个元素对应相乘

• 在矢量乘矢量的內积运算中，np.matmul 与np.dot没有区别，np.matmul中禁止矩阵与标量的乘法。

  https://blog.csdn.net/guaidoukx/article/details/97659074?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param