散列表是实现字典操作的一种有效数据结构,最坏情况的查找时间是$\theta (n)$,平均查找时间为$O(1)$。
散列表是普通数组概念的推广,数组可以直接寻址。
当实际存储的关键字数目比全部可能的关键字总数要小时,可以使用散列表来替代直接数组寻址。
直接寻址表 Direct-address table
关键字的全域U较小,没有两个元素具有相同的关键字。
使用数组,即直接寻址表,其中每个位置成为槽(slot),实际关键字集合K对应的槽指向对应的元素(关键字为k的元素存放在槽k中),其它槽为NIL,也可以使用其他关键字说明该槽为空。
缺点:如果全域U很大,计算机可能无法完整存储这张表;如果实际存储的关键字集合K相对于U来说很小,则T的大部分空间被浪费。
散列表
散列表需要的存储空间比直接寻址表少很多,关键字为k的元素存放在槽$h(k)$中。即:利用散列函数(hash function)h来计算出关键字为k的元素的槽的位置。散列函数将全域U映射到大小为m的散列表上,其中$m<<|U|$。
两个关键字可能被映射到同一个槽中,成为冲突(collision)。
通过链接法解决冲突:把映射到同一个槽中的关键字连成链表。
最坏情况:所有n个关键字都散列到同一个槽中,性能相当于普通链表。
平均情况:依赖于散列函数把n个关键字映射到m个槽位的平均程度。定义表T的装载因子$\alpha =n/m$。
在简单均匀散列(simple uniform hash)的情况下,一次查找的平均时间为$\theta(1+\alpha)$,说明总元素个数应该与表中元素个数成正比,则$\alpha=n/m=O(m)/m=O(1)$,此时查找操作平均需要常数时间。
当链表使用双向链表时,插入和删除的最坏情况也是$O(1)$,此时字典的全部操作都可以在常数时间完成。
散列函数
好的散列函数应该尽量满足简单均匀,尽量将相近的字符散列到不同的槽。
除法散列法
散列函数:$k(h) = k\% m$
注意:m不应该为2的幂。如果$m=2^p$,则$h(k)$就是k的二进制表示的p个最低位数字。设计散列函数时最好考虑所有位,因为无法保证各种最低p位的排列形式为等可能。m最好是一个不太接近2的幂的素数。
乘法散列法
散列函数:$\lfloor m(kA\%1)\rfloor$
其中常数A满足$0 < A < 1$。即:对kA的小数部分乘以m再向下取整。
优点:对于m的取值不是很关键。一般选择$A\approx (\sqrt5-1)/2=0.618…$
全域散列法 universal hashing
在一个函数组中随机地选择散列函数,使之独立于要存储的关键字,从而避免了将全部关键字散列到同一个槽中的最坏情况,选定后不再更改。
开放寻址法 open addressing
所有的元素都存放在散列表里,每个表项要么是u元素要么是NIL。散列表可能会填满,以至于无法再插入新的元素。该方法导致的一个结果是装载因子$\alpha$绝对不会超过1。槽中同样可以存放链表。
使用开放寻址法插入元素时,需要连续地检查散列表,或称为探查(probe),直到找到一个空槽来放置待插入的元素。
线性探查,二次探查,双重探查
完全散列
主要针对静态(static)的关键字集合,即:一旦各关键字存入表中,关键字集合就不再变化了。
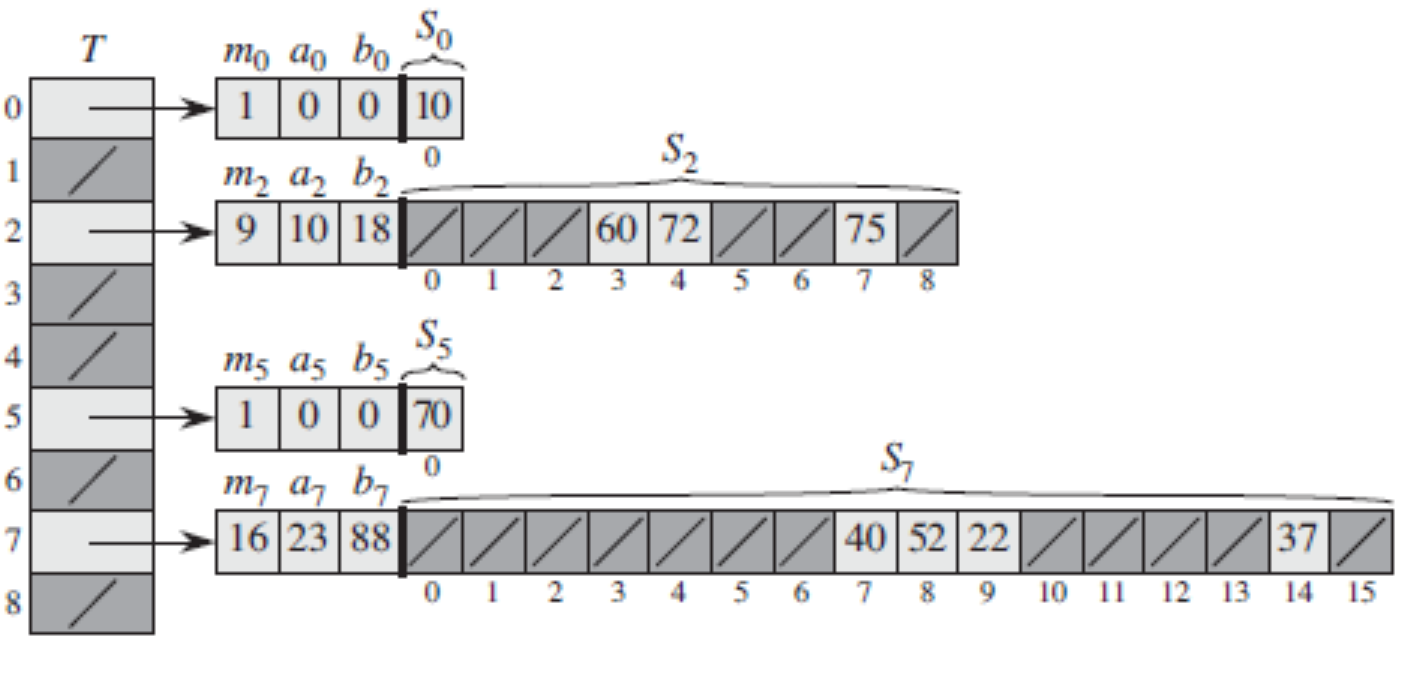
采用两级的散列方法来设计完全散列方案,每级上都使用全域散列。
为了保证不冲突,每个二级哈希表的数量是第一级映射到这个槽中元素个数的平方(在第 1 级,如果有$N_i$个元素映射到第i个槽,那么第$N_i$个槽对应的2级哈希表采用全域哈希。表的长度取$M_i = N_i^2$),这样可以保证整个哈希表非常的稀疏。
属性:将n个键映射到$n^2$个槽,如果从全域哈希H中随机选择h,那么期望的冲突次数小于1/2,不发生冲突的概率大于1/2。